
 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
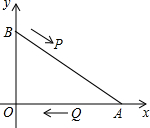 如圖,在直角坐標系中,已知點A(8,0)、B(0,6),點P由點B出發沿BA方向向點A作勻速直線運動,速度為每秒3個單位長度,點Q由A出發沿AO(O為坐標原點)方向向點O作勻速直線運動,速度為每秒2個單位長度,連接PQ,若設運動時間為t(0<t<$\frac{10}{3}$)秒.解答如下問題:
如圖,在直角坐標系中,已知點A(8,0)、B(0,6),點P由點B出發沿BA方向向點A作勻速直線運動,速度為每秒3個單位長度,點Q由A出發沿AO(O為坐標原點)方向向點O作勻速直線運動,速度為每秒2個單位長度,連接PQ,若設運動時間為t(0<t<$\frac{10}{3}$)秒.解答如下問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com