

分析 (1)過點M作MH⊥AB于H,MG⊥AD于G,連接AM,首先證明M是正方形ABCD對角線的交點,然后證明△MHF≌△MGE,利用全等三角形的性質得到ME=MF;
(2)過點M作ME⊥AB于E,MG⊥AD于G,利用矩形ABCD性質和已知條件證明∠HMF=∠GME,∠MGE=∠MHF,得出△MGE∽△MHF,然后利用相似三角形的性質即可求解;
(3)平行四邊形ABCD和平行四邊形QMNP中,∠M=∠B,AB=mBC,由于M是平行四邊形ABCD的對稱中心,MN交AB于F,AD交QM于E,則ME=mMF.證明方法和(1)(2)類似.
解答 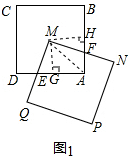 解:(1)ME=MF.
解:(1)ME=MF.
理由:如圖1,過點M作MH⊥AB于H,MG⊥AD于G,連接AM,則∠MHF=∠MGE=90°,
∵M是正方形ABCD的對稱中心,
∴AM平分∠BAD,
∴MH=MG,
在正方形ABCD中,∠DAB=90°,而∠MHA=∠MGA=90°,
∴∠EMF=∠HMG=90°,
∴∠FMH=∠EMG,
在△MHF和△MGE中,
$\left\{\begin{array}{l}{∠FMH=∠EMG}\\{MH=MG}\\{∠MHF=∠MGE}\end{array}\right.$
∴△MHF≌△MGE(ASA),
∴MF=ME,
故答案為:MF=ME;
(2)MF=2ME.
理由:如圖2,過點M作MG⊥AB于G,MH⊥AD于H,則∠MHE=∠MGF=90°,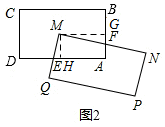
在矩形ABCD中,∠A=90°,
∴在四邊形GMHA中,∠GMH=90°,
又∵∠EMF=90°,
∴∠HME=∠GMF,
又∵∠MGF=∠MHE=90°,
∴△MGF∽△MHE,
∴$\frac{ME}{MF}$=$\frac{MH}{MG}$,
又∵M是矩形ABCD的對稱中心,
∴MG=$\frac{1}{2}$BC,MH=$\frac{1}{2}$AB,
∴$\frac{MH}{MG}$=$\frac{AB}{BC}$=$\frac{1}{2}$,
∴MF=2ME;
(3)ME:MF=m.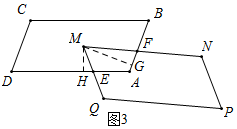
理由:如圖3,過點M作MG⊥AB于G,MH⊥AD于H,則∠MHE=∠MGF=90°,
在平行四邊形ABCD中,∠A+∠B=180°,而∠EMF=∠B,
∴∠A+∠EMF=180°,
又∵在四邊形AGMH中,∠A+∠HMG=180°,
∴∠EMF=∠GMF,
又∵∠MGF=∠MHE=90°,
∴△MGF∽△MHE,
∴$\frac{ME}{MF}$=$\frac{MH}{MG}$,
又∵M是矩形ABCD的對稱中心,
∴$\frac{MH}{MG}$=$\frac{AB}{BC}$=$\frac{mBC}{BC}$=m,
∴ME:MF=m.
點評 此題屬于四邊形綜合題,主要考查了正方形、矩形、平行四邊形的性質、全等三角形、相似三角形的性質和判定的綜合應用,解決問題的關鍵是作輔助線構造全等三角形或相似三角形,運用相似三角形的對應邊成比例進行推導.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:填空題
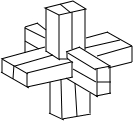 魯班鎖是中國傳統的智力玩具.起源于古代漢族建筑中首創的榫卯結構.這種三維的拼插器具內部的凹凸部分(即榫卯結構)嚙合十分巧妙.外觀看是嚴絲合縫的十字立方體,其上下、左右、前后完全對稱.從外表上看,六根等長的正四棱柱體分成三組,經90°榫卯起來,如圖,若正四棱柱體的高為6,底面正方形的邊長為1,現將該魯班鎖放進一個球形容器內,則該球形容器的表面積的最小值為96.(容器壁的厚度忽略不計)
魯班鎖是中國傳統的智力玩具.起源于古代漢族建筑中首創的榫卯結構.這種三維的拼插器具內部的凹凸部分(即榫卯結構)嚙合十分巧妙.外觀看是嚴絲合縫的十字立方體,其上下、左右、前后完全對稱.從外表上看,六根等長的正四棱柱體分成三組,經90°榫卯起來,如圖,若正四棱柱體的高為6,底面正方形的邊長為1,現將該魯班鎖放進一個球形容器內,則該球形容器的表面積的最小值為96.(容器壁的厚度忽略不計)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1,2,$\sqrt{6}$ | B. | 3,5,4 | C. | 5,12,13 | D. | 3,2,$\sqrt{13}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com