
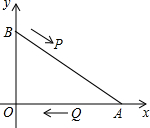
 如圖,在直角坐標系中,已知點A(8,0)、B(0,6),點P由點B出發沿BA方向向點A作勻速直線運動,速度為每秒3個單位長度,點Q由A出發沿AO(O為坐標原點)方向向點O作勻速直線運動,速度為每秒2個單位長度,連接PQ,若設運動時間為t(0<t<$\frac{10}{3}$)秒.解答如下問題:
如圖,在直角坐標系中,已知點A(8,0)、B(0,6),點P由點B出發沿BA方向向點A作勻速直線運動,速度為每秒3個單位長度,點Q由A出發沿AO(O為坐標原點)方向向點O作勻速直線運動,速度為每秒2個單位長度,連接PQ,若設運動時間為t(0<t<$\frac{10}{3}$)秒.解答如下問題:分析 (1)分兩種情形討論①當$\frac{PA}{AB}$=$\frac{AQ}{OA}$時,△APQ∽△ABO,②當$\frac{AP}{OA}$=$\frac{AQ}{AB}$時,△APQ∽△AOB,分別列出方程計算即可.
(2)過點P作過點P作PD⊥x軸于點D,構造平行線PD∥BO,由線段比例關系 $\frac{AP}{AB}$=$\frac{PD}{OB}$ 求得PD,依據三角形的面積公式可求得S與t之間的函數關系式是一個關于t的二次函數,利用二次函數求極值的方法求出S的最大值.
解答 解:(1)如圖①中,
在Rt△ABO中,由勾股定理得:AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=10.
①當$\frac{PA}{AB}$=$\frac{AQ}{OA}$時,△APQ∽△ABO,
即$\frac{10-3t}{10}$=$\frac{2t}{8}$,t=$\frac{20}{11}$.
②當$\frac{AP}{OA}$=$\frac{AQ}{AB}$時,△APQ∽△AOB,
即$\frac{10-3t}{8}$=$\frac{2t}{10}$,t=$\frac{50}{23}$,
綜上所述,t=$\frac{20}{11}$s或$\frac{50}{23}$s時,△PAQ與△AOB相似.
(2)如圖②所示:過點P作PD⊥x軸于點D.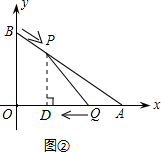
∵PD⊥x軸,OB⊥x軸,
∴OB∥PD.
∴$\frac{AP}{AB}$=$\frac{PD}{OB}$,即 $\frac{10-3t}{10}$=$\frac{PD}{6}$.
∴PD=6-$\frac{9}{5}$t.
由三角形的面積公式可知:S=$\frac{1}{2}$AQ•PD=$\frac{1}{2}$•2t•(6-$\frac{9}{5}$t)=6t-$\frac{9}{5}$t2.
∴S與t的函數關系式為y=-$\frac{9}{5}$t2+6t.
∴S=-$\frac{9}{5}$(t-$\frac{5}{3}$)2+5.
∴當t=$\frac{5}{3}$s時,S有最大值,最大值為5(平方單位).
點評 本題主要考查的是動點問題的函數圖象、配方法求二次函數的最值、相似三角形的判定和性質等知識,解題的關鍵是學會用分類討論的思想思考問題,靈活運用所學知識解決問題,屬于中考常考題型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | 長方形的長一定時,其面積y與寬x | |
| B. | 高速公路上勻速行駛的汽車,其行駛的路程y與行駛的時間x | |
| C. | y=|x| | |
| D. | |y|=x |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
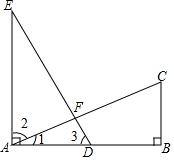 如圖,已知EA⊥AB,BC∥EA,EA=AB=2BC,D為AB的中點,則下面式子中不能成立的是( )
如圖,已知EA⊥AB,BC∥EA,EA=AB=2BC,D為AB的中點,則下面式子中不能成立的是( )| A. | ∠1+∠3=90° | B. | DE⊥AC且DE=AC | C. | ∠3=60° | D. | ∠2=∠3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖所示,將一副三角板疊放在一起,使直角的頂點重合于點O
如圖所示,將一副三角板疊放在一起,使直角的頂點重合于點O查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com