
分析 已知△ABC是等腰三角形,根據等腰三角形的性質,若過A作底邊BC的垂線,則AD必過圓心O,在Rt△OBD中,用半徑表示出OD的長,即可用勾股定理求得半徑的長.
解答 解:過A作AD⊥BC于D,連接BO,
△ABC中,AB=AC,AD⊥BC,
則AD必過圓心O,
Rt△ABD中,AB=5,BD=3 ,
,
∴AD=4
設⊙O的半徑為x,
Rt△OBD中,OB=x,OD=4-x,
根據勾股定理,得:OB2=OD2+BD2,
即:x2=(4-x)2+32,
解得:x=$\frac{25}{8}$,
故答案為:$\frac{25}{8}$.
點評 本題考查了三角形的外接圓、等腰三角形的性質和勾股定理等知識的綜合應用,正確畫出滿足題意的圖形并做出輔助線是解題的關鍵.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
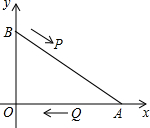 如圖,在直角坐標系中,已知點A(8,0)、B(0,6),點P由點B出發沿BA方向向點A作勻速直線運動,速度為每秒3個單位長度,點Q由A出發沿AO(O為坐標原點)方向向點O作勻速直線運動,速度為每秒2個單位長度,連接PQ,若設運動時間為t(0<t<$\frac{10}{3}$)秒.解答如下問題:
如圖,在直角坐標系中,已知點A(8,0)、B(0,6),點P由點B出發沿BA方向向點A作勻速直線運動,速度為每秒3個單位長度,點Q由A出發沿AO(O為坐標原點)方向向點O作勻速直線運動,速度為每秒2個單位長度,連接PQ,若設運動時間為t(0<t<$\frac{10}{3}$)秒.解答如下問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 學校要圍一個矩形花圃,其一邊利用足夠長的墻,另三邊用籬笆圍成,由于園藝需要,還要用一段籬笆將花圃分隔為兩個小矩形部分(如圖所示),總共36米的籬笆恰好用完(不考慮損耗).設矩形垂直于墻面的一邊AB的長為x米(要求AB<AD),矩形花圃ABCD的面積為S平方米.
學校要圍一個矩形花圃,其一邊利用足夠長的墻,另三邊用籬笆圍成,由于園藝需要,還要用一段籬笆將花圃分隔為兩個小矩形部分(如圖所示),總共36米的籬笆恰好用完(不考慮損耗).設矩形垂直于墻面的一邊AB的長為x米(要求AB<AD),矩形花圃ABCD的面積為S平方米.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com