
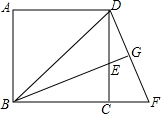
 如圖,已知正方形ABCD中,BE平分∠DBC且交CD邊于點(diǎn)E,將△BCE繞點(diǎn)C順時針旋轉(zhuǎn)到△DCF的位置,并延長BE交DF于點(diǎn)G.
如圖,已知正方形ABCD中,BE平分∠DBC且交CD邊于點(diǎn)E,將△BCE繞點(diǎn)C順時針旋轉(zhuǎn)到△DCF的位置,并延長BE交DF于點(diǎn)G.分析 (1)由性質(zhì)得出△BCE≌△DCF,即:∠CBE=∠CDF,再用直角三角形的性質(zhì)進(jìn)行等量代換即可得出結(jié)論;
(2)借助(1)的結(jié)論和角平分線的意義,即可判斷出△BDG∽△DEG,得出結(jié)論;
(3)先利用角平分線定理得出DE=$\sqrt{2}$CE,再用勾股定理的課得出BC=($\sqrt{2}$+1)CE,進(jìn)而得出BE=$\sqrt{2(2+\sqrt{2})}$CE,再有已知條件得出BE=2$\sqrt{3(2-\sqrt{2})}$,即可求出CE,進(jìn)而求出BC即可得出正方形的面積.
解答 解:(1)∵四邊形ABCD是正方形,
∴∠BCD=90°,
∴∠CBE+∠CEB=90°,
∵△BCE繞點(diǎn)C順時針旋轉(zhuǎn)到△DCF的位置,
∴ △BCE≌△DCF,
△BCE≌△DCF,
∴∠CBE=∠CDF,
∴∠CDF+∠CEB=90°,
∵∠DEG=∠CEB,
∴∠DEG+∠CDF=90°,
∴∠BGD=90°,
∴BG⊥DF,
(2)$\frac{DG}{EG}=\frac{BD}{DE}$;
理由:由(1)知,∠CBE=∠CDF,
∵BE平分∠DBC,
∴∠CBE=∠DBE,
∴∠CDF=∠DBE,
∵∠DGE=∠BGD,
∴△BDG∽△DEG,
∴$\frac{DG}{EG}=\frac{BG}{DG}$=$\frac{BD}{DE}$,
即:$\frac{DG}{EG}=\frac{BD}{DE}$;
(3)∵BD是正方形ABCD的對角線,
∴BD=$\sqrt{2}$BC=$\sqrt{2}$CD,
∵BE平分∠DBC,
∴$\frac{BC}{BD}=\frac{CE}{DE}$=$\frac{1}{\sqrt{2}}$,
∴DE=$\sqrt{2}$CE,
∴BC=CD=CE+DE=CE+$\sqrt{2}$CE=($\sqrt{2}$+1)CE,
在Rt△BCE中,BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=$\sqrt{(\sqrt{2}+1)^{2}C{E}^{2}+C{E}^{2}}$=$\sqrt{2(2+\sqrt{2})}$CE,
由(2)知,△BDG∽△DEG,
∴$\frac{DG}{EG}=\frac{BG}{DG}$,
∴DG2=EG•BG,
∵EG•BG=3(2-$\sqrt{2}$),
∴DG=$\sqrt{3(2-\sqrt{2})}$,
由(1)知,BG⊥DF,
∵BE平分∠DBC,
∴DF=2DE=2$\sqrt{3(2-\sqrt{2})}$,
由(1)知,△BCE≌△DCF,
∴BE=DF=2$\sqrt{3(2-\sqrt{2})}$,
∵BE=$\sqrt{2(2+\sqrt{2})}$CE,
∴2$\sqrt{3(2-\sqrt{2})}$=$\sqrt{2(2+\sqrt{2})}$CE,
∴CE=$\frac{2\sqrt{3(2-\sqrt{2})}}{\sqrt{2(2+\sqrt{2})}}$=$\sqrt{3}$(2-$\sqrt{2}$),
∴S正方形ABCD=BC2=($\sqrt{2}$+1)2CE2=($\sqrt{2}$+1)2×[$\sqrt{3}$(2-$\sqrt{2}$)]2=6,
即:正方形ABCD面積為6.
點(diǎn)評 此題是四邊形綜合題,主要考查了正方形的性質(zhì),旋轉(zhuǎn)的性質(zhì),角平分線定理,相似三角形相似性質(zhì)和判定,全等三角形的判定和性質(zhì),勾股定理等知識點(diǎn),(2)中判斷出△BDG∽△DEG和(3)求出DG是解答關(guān)鍵.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | m | B. | n | C. | 12 | D. | m與n的積 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
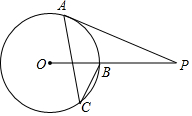 如圖,PA切⊙O于點(diǎn)A,PO交⊙O于點(diǎn)B,點(diǎn)C是優(yōu)弧AB上一點(diǎn),若∠ACB=35°,則∠P的度數(shù)是20°.
如圖,PA切⊙O于點(diǎn)A,PO交⊙O于點(diǎn)B,點(diǎn)C是優(yōu)弧AB上一點(diǎn),若∠ACB=35°,則∠P的度數(shù)是20°.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com