
 如圖,在四邊形ABCD中,AD∥BC,DE⊥BC,垂足為點E,連接AC交DE于點F,點G為AF的中點,∠ACD=2∠ACB.若DG=3,EC=1,則DE的長為( )
如圖,在四邊形ABCD中,AD∥BC,DE⊥BC,垂足為點E,連接AC交DE于點F,點G為AF的中點,∠ACD=2∠ACB.若DG=3,EC=1,則DE的長為( )| A. | $\sqrt{12}$ | B. | $\sqrt{10}$ | C. | $\sqrt{8}$ | D. | $\sqrt{6}$ |
分析 根據直角三角形斜邊上的中線的性質可得DG=AG,根據等腰三角形的性質可得∠GAD=∠GDA,根據三角形外角的性質可得∠CGD=2∠GAD,再根據平行線的性質和等量關系可得∠ACD=∠CGD,根據等腰三角形的性質可得CD=DG,再根據勾股定理即可求解.
解答 解:∵AD∥BC,DE⊥BC,
∴AD⊥DE,
∵G為AF的中點,即DG為斜邊AF的中線,
∴DG=AG=FG=3,
∴∠GAD=∠GDA,
∵AD∥BC,
∴∠GAD=∠ACB,
設∠ACB=α,則∠ACD=2α,
∵∠GAD=∠GDA=α,
∴∠DGC=2α,即∠ACD=∠DGC,
∴DG=DC=3,
在Rt△DEC中,DC=3,EC=1,
根據勾股定理得:DE=$\sqrt{D{C}^{2}-E{C}^{2}}$=$\sqrt{8}$,
故選C.
點評 本題考查了勾股定理,直角三角形斜邊上中線性質,直角三角形的性質的應用,平行線的性質,解此題的關鍵是證出DG=DC.


科目:初中數學 來源:2016-2017學年北京市西城區七年級上學期期末考試數學試卷(解析版) 題型:填空題
觀察下面的圖形(每個正方形的邊長均為1)和相應的等式,探究其中的規律:
①
 1×
1× =1-
=1-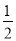
②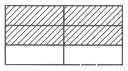
 2×
2×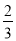 =2-
=2-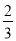
③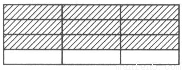
 3×
3×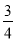 =3-
=3-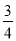
……
(1)在下面給出的四個正方形中畫出第四個圖形,并在右邊寫出與之對應的等式;

 _______________
_______________
(2)猜想并寫出與第幾個圖形相對應的等式:______________________________。
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,正方形ABCD的四個頂點分別在四條平行線l1,l2,l3,l4上,AD,BC邊分別與l2,l3相交于點F,E,這四條直線中相鄰兩條之間的距離依次為a,b,c(a>0,b>0,c>0),且AB邊于直線l2的夾角為α,則下列結論錯誤的是( )
如圖,正方形ABCD的四個頂點分別在四條平行線l1,l2,l3,l4上,AD,BC邊分別與l2,l3相交于點F,E,這四條直線中相鄰兩條之間的距離依次為a,b,c(a>0,b>0,c>0),且AB邊于直線l2的夾角為α,則下列結論錯誤的是( )| A. | a=c | B. | 當a=b=c時,四邊形BEDF是菱形 | ||
| C. | $\frac{AF}{AB}$=$\frac{a}{a+b}$ | D. | 正方形ABCD面積為(a+b)2+c2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
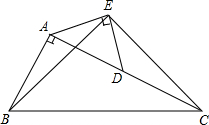 已知:如圖,在Rt△ABC中,∠BAC=90°,AC=2AB,點D是AC的中點,以AD為斜邊在△ABC外作等腰直角三角形AED,連結BE、EC.試猜想線段BE和EC有何關系,并證明你的猜想.
已知:如圖,在Rt△ABC中,∠BAC=90°,AC=2AB,點D是AC的中點,以AD為斜邊在△ABC外作等腰直角三角形AED,連結BE、EC.試猜想線段BE和EC有何關系,并證明你的猜想.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 等腰三角形 | B. | 等邊三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知在等腰直角三角形ABC中,∠CAB=90°,以AB為邊向外作等邊△ABD,AE⊥BD,CD、AE交于點M,若DM=1,求BC的值.
如圖,已知在等腰直角三角形ABC中,∠CAB=90°,以AB為邊向外作等邊△ABD,AE⊥BD,CD、AE交于點M,若DM=1,求BC的值.查看答案和解析>>
科目:初中數學 來源:2016-2017學年北京市西城區七年級上學期期末考試數學試卷(解析版) 題型:單選題
如圖所示,用量角器度量一些角的度數。下列結論中正確的是( )
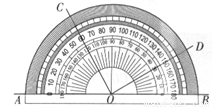
A. ∠BOC=60° B. ∠COD=150°
C. ∠AOC與∠BOD的大小相等 D. ∠AOC與∠BOD互余
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com