
分析 由關于x的一元二次方程(1-m)x2+4x+1=0有兩個不相等的實數根,根據一元二次方程的定義和根的判別式的意義可得1-m≠0且△>0,兩個不等式的公共解即為m的取值范圍.
解答 解:∵關于x的方程(1-m)x2+4x+1=0有兩個不相等的實數根,
∴1-m≠0且△>0,即42-4•(1-m)•1>0,
解得m>-3且m≠1,
∴m的取值范圍為m>-3且m≠1.
故答案為:m>-3且m≠1.
點評 本題考查了一元二次方程ax2+bx+c=0(a≠0)的根的判別式△=b2-4ac,關鍵是熟記當△>0,方程有兩個不相等的實數根;當△<0,方程有兩個相等的實數根;當△=0,方程沒有實數根.


科目:初中數學 來源: 題型:選擇題
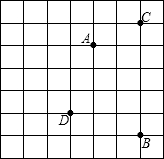 如圖,大正方形是由邊長為1的小正方形拼成的,A,B,C,D四個點是小正方形的頂點,以其中三個點為頂點,可以構成直角三角形的個數是( )
如圖,大正方形是由邊長為1的小正方形拼成的,A,B,C,D四個點是小正方形的頂點,以其中三個點為頂點,可以構成直角三角形的個數是( )| A. | 2 | B. | 1 | C. | 4 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
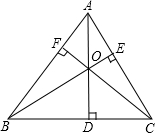 如圖,△ABC的三條高AD、BE、CF相交于點O.
如圖,△ABC的三條高AD、BE、CF相交于點O.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 矩形 | B. | 菱形 | ||
| C. | 正方形 | D. | 不是矩形、菱形的四邊形 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
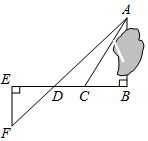 為了測量被池塘隔開的A,B兩點之間的距離,根據實際情況,作出如圖所示的圖形,其中AB⊥BE,EF⊥BE,AF交BE于點D,C在BD上,有四位同學分別測量出以下四組數據:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根據所測數據,求出A、B間距離的有( )
為了測量被池塘隔開的A,B兩點之間的距離,根據實際情況,作出如圖所示的圖形,其中AB⊥BE,EF⊥BE,AF交BE于點D,C在BD上,有四位同學分別測量出以下四組數據:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根據所測數據,求出A、B間距離的有( )| A. | 4組 | B. | 3組 | C. | 2組 | D. | 1組 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com