
 如圖,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于點D,AE⊥AB交BC于點E.若S△ABC=m2+9n2,S△ADE=mn,則m與n之間的數量關系是( )
如圖,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于點D,AE⊥AB交BC于點E.若S△ABC=m2+9n2,S△ADE=mn,則m與n之間的數量關系是( )| A. | m=3n | B. | m=6n | C. | n=3m | D. | n=6m |
分析 設AD=x,由等腰三角形性質知∠B=30°,利用三角函數求得BD=$\frac{AD}{tanB}$=$\sqrt{3}$x、AB=2AD=2x,BC=2BD=2$\sqrt{3}$x,在Rt△ABE中求得BE=$\frac{4\sqrt{3}}{3}$x知DE=BE-BD=$\frac{\sqrt{3}}{3}$x,由$\frac{{S}_{△ABC}}{{S}_{△ADE}}$=6得m2+9n2=6mn,即(m-3n)2=0,可知答案.
解答 解:設AD=x,
∵AB=AC,∠BAC=120°,
∴∠B=30°,
在Rt△ABD中,BD=$\frac{AD}{tanB}$=$\frac{x}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$x,AB=2AD=2x,
則BC=2BD=2$\sqrt{3}$x,
在Rt△ABE中,BE=$\frac{AB}{cosB}$$\frac{2x}{\frac{\sqrt{3}}{3}}$=$\frac{4\sqrt{3}}{3}$x,
∴DE=BE-BD=$\frac{\sqrt{3}}{3}$x,
∵$\frac{{S}_{△ABC}}{{S}_{△ADE}}$=$\frac{\frac{1}{2}•2\sqrt{3}x•x}{\frac{1}{2}•\frac{\sqrt{3}}{3}x•x}$=6,
∴m2+9n2=6mn,即(m-3n)2=0,
∴m=3n,
故選:A.
點評 本題主要考查等腰三角形的性質及解直角三角形,根據三角函數及等腰三角形的性質得出S△ABC=6S△ADE是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 兩點確定一條直線 | B. | 垂線段最短 | ||
| C. | 兩點之間線段最短 | D. | 三角形兩邊之和大于第三邊 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
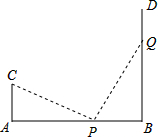 如圖,AB=9cm,CA⊥AB于A,DB⊥AB于B,且AC=3m,P點從B向A運動,每分鐘走1m,Q點從B向D運動,每分鐘走2m,P、Q兩點同時出發,運動3分鐘后△CAP與△PQB全等.
如圖,AB=9cm,CA⊥AB于A,DB⊥AB于B,且AC=3m,P點從B向A運動,每分鐘走1m,Q點從B向D運動,每分鐘走2m,P、Q兩點同時出發,運動3分鐘后△CAP與△PQB全等.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 盤秤是一種常見的稱量工具,指針轉過的角度與被稱物體的重量有一定的關系,如下表所示:
盤秤是一種常見的稱量工具,指針轉過的角度與被稱物體的重量有一定的關系,如下表所示:| 重量(單位:千克) | 0 | 1 | 2 | 2.5 | 3 | … | b |
| 指針轉過的角度 | 0° | 18° | 36° | a° | 54° | … | 180° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a(x1-x2)=d | B. | a(x2-x1)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com