Question

16．在等邊△ABC中，AB=8，P為AB的中點(diǎn)，小慧拿著含60°角的透明三角板，使60°角的頂點(diǎn)落在點(diǎn)P，將三角形繞點(diǎn)P旋轉(zhuǎn)，三角形兩邊與線(xiàn)段AC交于點(diǎn)F，與射線(xiàn)BC交于點(diǎn)E．
（1）如圖1，當(dāng)∠APF=60°時(shí)，AF•BE=16，如圖2，當(dāng)∠APF=30°時(shí)，AF•BE=16；
（2）如圖3，當(dāng)30°＜∠APF＜60°時(shí)，小慧多次嘗試，得到一個(gè)猜想，AF•BE的值是一個(gè)常數(shù)，你認(rèn)為小慧的猜想正確嗎？若正確，請(qǐng)寫(xiě)出這個(gè)常數(shù)并給出證明，若不正確，請(qǐng)說(shuō)明理由．
（3）如圖4，當(dāng)0°＜∠PAF＜30°時(shí)，連結(jié)EF，設(shè)EF=m，請(qǐng)用含m的式子表示PF•PE的值．

Answer 1

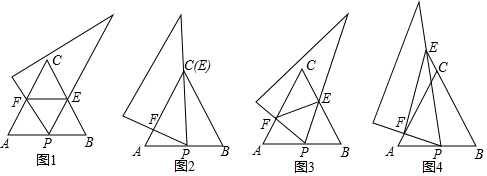
分析 （1）由等邊三角形的性質(zhì)得出AP=BP=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4，當(dāng)∠APF=60°時(shí)，證出△APF是等邊三角形，得出AF=AP=4，再證明△PBE是等邊三角形，得出BE=BP=4，因此AF•BE=16．當(dāng)∠APF=30°時(shí)，證明△APF是直角三角形，得出AF=$\frac{1}{2}$AP=2，求出BE=BC=AB=8，得出AF•BE=2×8=16即可；
（2）證出∠APF=∠BEF，得出△APF～△BEF，得出$\frac{AF}{AP}=\frac{PB}{BE}$，即可得出結(jié)論；
（3）由旋轉(zhuǎn)易證：∠APF=∠PEF，證明△APF～△PPE，得出$\frac{PF}{AP}=\frac{EF}{PE}$，即可得出結(jié)論．

解答 解：（1）∵△ABC是等邊三角形，P為AB的中點(diǎn)，
∴AP=BP=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4，
如圖1，當(dāng)∠APF=60°時(shí)，
∵∠PAF=60°，
∴△APF是等邊三角形，
∴AF=AP=4，
∵∠FPE=60°，
∴∠EPB=180°-∠APF-∠FPE=180°-60°-60°=60°，
∵∠PBE=60°，
∴△PBE是等邊三角形，
∴BE=BP=4，
∴AF•BE=4×4=16．
如圖2，當(dāng)∠APF=30°時(shí)，
∵∠PAF=60°，
∴△APF是直角三角形，
∴AF=$\frac{1}{2}$AP=2，
∵BE=BC=AB=8，
∴AF•BE=2×8=16；
故答案為：16，16．
（2）如圖3，當(dāng)30°＜∠APF＜60°時(shí)，小慧的猜想是正確的．這個(gè)常數(shù)是16．理由如下：
∵∠EPB=180°-∠APF-∠FPE=180°-∠APF-60°=120°-∠APF，
又∵∠EPB=180°-∠PBE-∠BEP=180°-60°-∠BEF=120°-∠BEF，
∴∠APF=∠BEF，
∴△APF～△BEF，
∴$\frac{AF}{AP}=\frac{PB}{BE}$，
∴AF•BE=AP•PB=4×4=16（常數(shù)）．
（3）由旋轉(zhuǎn)的性質(zhì)得出：∠APF=∠PEF，
∵∠FAP=∠FPE=60°，
∴△APF～△PPE，
∴$\frac{PF}{AP}=\frac{EF}{PE}$，
∴PF•PE=AP•EF=4m．

點(diǎn)評(píng) 本題主要考查了全等三角形的判定和等邊三角形的性質(zhì)，注意對(duì)全等三角形和等邊三角形的應(yīng)用．