
 在平面直角坐標系xOy中,頂點D在第一象限的拋物線y=-x2-kx-(k-1)與x軸交于A(x1,0)、B(x2,0)兩點(點A在點B的左側,OA<OB),交y 軸于點C,且x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10.
在平面直角坐標系xOy中,頂點D在第一象限的拋物線y=-x2-kx-(k-1)與x軸交于A(x1,0)、B(x2,0)兩點(點A在點B的左側,OA<OB),交y 軸于點C,且x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10.分析 (1)利用拋物線對應的一元二次方程兩根之間關系求出K值,代回拋物線,驗算滿足頂點D在第一象限即可求出拋物線解析式;
(2)利用三角形外心性質求出P的坐標,設出PQ直線解析式,聯立方程組,求出點P、Q坐標,利用兩點間距離公式,求出相似三角形對應線段的長,分類討論相似三角形,即可求出點R的坐標;
(3)求出直線BD解析式及線段BD長度,由題意知BD=KN,設出點N點K坐標,利用等腰三角形性質求出點M坐標;
解答 解:(1)令y=0,
-x2-kx-(k-1)=0,
∴(x-1)[x+(k-1)]=0,
∴x=1或x=1-k,
∵x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10,
∴1+(1-k)2=10.
解得:k=4,或k=-2,
當k=4,拋物線為y=-x2-4x-3,
頂點D橫坐標為-2,不在第一象限,舍去,
當k=-2時,拋物線解析式為:y=-x2+2x+3,
頂點坐標D(1,4),
∴拋物線解析式為:y=-x2+2x+3.
(2)由(1)得:A(-1,0),B(3,0),C(0,3),
∴線段AB垂直平分線為直線x=1,
線段BC的垂直平分線為直線y=x,
聯立得P(1,1),
直線AC解析式為:y=3x+3,
設直線PQ:y=kx+b,代入(1,1),
得y=kx+1-k,
令y=0,x=$\frac{k-1}{k}$,
∴R($\frac{k-1}{k}$,0)
聯立:直線AC和QR
求得Q($\frac{2+k}{k-3}$,$\frac{6k-3}{k-3}$),
利用勾股定理求得:
AC=$\sqrt{10}$,AB=4,AQ=$\sqrt{(-1-\frac{2+k}{k-3})^{2}+(\frac{6k-3}{k-3})^{2}}$),AR=$\frac{k-1}{k}$+1
當△ARQ∽△ABC時,
$\frac{AC}{AQ}$=$\frac{AB}{AR}$,解得:k=-1,
∴R(2,0).
當△ARQ∽△ACB時,
$\frac{AC}{AR}=\frac{AB}{AQ}$,解得k=-2,
∴R($\frac{3}{2}$,0).
∴R的坐標為R($\frac{3}{2}$,0)或R(2,0).
(3)設直線BD解析式為y=kx+b,
∵B(3,0),D(1,4),
代入直線解析式得:k=-2,b=6,
∴直線BD解析式為y=-2x+6,
BD=$\sqrt{{4}^{2}+(3-1)^{2}}$=2$\sqrt{5}$,
設點M(0.b),
當BM=BD=2$\sqrt{5}$,
∴OM=$\sqrt{B{M}^{2}-O{B}^{2}}$=$\sqrt{20-9}$=$\sqrt{11}$,
∴M(0,$\sqrt{11}$.
當BD=BM時,根據拋物線對稱性,點M在y軸負半軸,不符合題意.
當BM=DM時,
$\sqrt{9+{b}^{2}}$=$\sqrt{1+(4-b)^{2}}$,
解得:b=1,
∴M(0,1).
綜上所述,點M坐標為(0,1)或(0,$\sqrt{11}$).
點評 題目考查的二次函數的綜合應用,通過對二次函數一次函數解析式的求解,結合相似三角形,考查學生解決綜合問題的能力,題目整體較難,屬于壓軸題,適合學生針對中考壓軸訓練.


科目:初中數學 來源: 題型:解答題
 如圖,AB是⊙O的直徑,點D是⊙O上一點,點C是弧AD的中點,連接AC、BD、AD、BC交于點Q.
如圖,AB是⊙O的直徑,點D是⊙O上一點,點C是弧AD的中點,連接AC、BD、AD、BC交于點Q.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
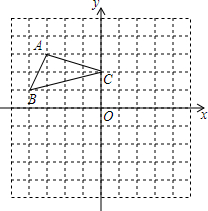 方格紙中每個小正方形的邊長都是1個單位長度,△ABC在平面直角坐標系中的位置如圖所示.
方格紙中每個小正方形的邊長都是1個單位長度,△ABC在平面直角坐標系中的位置如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| x | … | … | ||||||||||
| y | … | … |

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
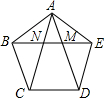 如圖,在正五邊形ABCDE中,對角線AD、AC與EB分別交于點M、N.
如圖,在正五邊形ABCDE中,對角線AD、AC與EB分別交于點M、N.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 90 | B. | 80 | C. | 70 | D. | 60 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com