
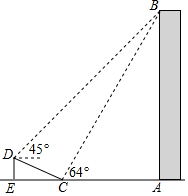
 如圖,在大樓AB的正前方有一斜坡CD長為13米,坡度為1:$\frac{12}{5}$,高為DE.在斜坡底的點C處測得樓頂B的仰角為64°,在斜坡頂的點D處測得樓頂B的仰角為45°,其中點A、C、E在同一直線上,求斜坡的高 DE與大樓AB的高度.(參考數據:sin64°≈0.9,tan64°≈2)
如圖,在大樓AB的正前方有一斜坡CD長為13米,坡度為1:$\frac{12}{5}$,高為DE.在斜坡底的點C處測得樓頂B的仰角為64°,在斜坡頂的點D處測得樓頂B的仰角為45°,其中點A、C、E在同一直線上,求斜坡的高 DE與大樓AB的高度.(參考數據:sin64°≈0.9,tan64°≈2) 分析 由斜坡CD坡度為1:$\frac{12}{5}$即DE:CE=5:12,設DE=5x,則CE=12x,在Rt△CDE中根據勾股定理求得x的值,即可知DE、CE的長;過點D作DF⊥AB于F,則AF=DE=5米,設BF=DF=a,則AC=AE-CE=DF-CE=a-12,AB=AF+BF=5+a,在Rt△ABC中,根據tan∠ACB=$\frac{AB}{AC}$可求得a的值,繼而可得AB的長.
解答 解:∵斜坡CD坡度為1:$\frac{12}{5}$,即DE:CE=5:12,
設DE=5x,則CE=12x,
∵CD=13,
在Rt△CDE中,DE2+CE2=CD2,即(5x)2+(12x)2=132,
解得:x=-1(舍)或x=1,
故DE=5米,CE=12米;
過點D作DF⊥AB于F,
則AF=DE=5米,
∵∠BDF=45°,
∴設BF=DF=a,
則AC=AE-CE=DF-CE=a-12,AB=AF+BF=5+a,
在Rt△ABC中,∵tan∠ACB=$\frac{AB}{AC}$,
∴$\frac{5+a}{a-12}$=2,
解得:a=29,
∴AB=BF+AF=29+5=34米,
答:斜坡CD的高度DE為5米,大樓的高AB為34米.
點評 本題主要考查解直角三角形的應用-坡度、坡角和仰角、俯角的問題,此類題目要求學生借助仰角構造直角三角形,并結合圖形利用三角函數解直角三角形.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | a2 | C. | -a | D. | $\frac{1}{a^2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 固定費用(元) | 免費撥打時間(分鐘) | 超出免費時間后單價(元/分鐘) | |
| A | 18 | 1500 | 0.1 |
| B | 38 | 4000 | 0.07 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2016-2017學年北京市西城區七年級上學期期末考試數學試卷(解析版) 題型:單選題
下列運算中,正確的是( )
A. 4x+3y=7xy B. 3x2+2=5x2
C. 6xy-4xy=2xy D. 5x2-x2=4
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
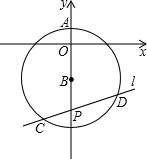 如圖,圓心在y軸的負半軸上,半徑為5的⊙B與y軸的正半軸交于點A(0,1),過點P(0,-7)的直線l與⊙B相交于C,D兩點,則弦CD長的所有可能的整數值有3個.
如圖,圓心在y軸的負半軸上,半徑為5的⊙B與y軸的正半軸交于點A(0,1),過點P(0,-7)的直線l與⊙B相交于C,D兩點,則弦CD長的所有可能的整數值有3個.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (2-x)(2+x)=4-x2 | B. | -a(a-b)=-a2+ab | C. | m2-n2=(m+n)(m-n) | D. | (1-x)2=(x-1)2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com