
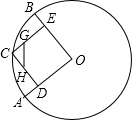
 在⊙O中,半徑OA、OB互相垂直,點C為弧$\widehat{AB}$上一點(不與A、B重合),CD⊥OA,CE⊥OB,垂足分別為D、E,點G、H分別在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,當C點在弧$\widehat{AB}$上順時針運動時,已知⊙O的半徑長為6,則GH的長度為( )
在⊙O中,半徑OA、OB互相垂直,點C為弧$\widehat{AB}$上一點(不與A、B重合),CD⊥OA,CE⊥OB,垂足分別為D、E,點G、H分別在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,當C點在弧$\widehat{AB}$上順時針運動時,已知⊙O的半徑長為6,則GH的長度為( )| A. | 3 | B. | 2 | C. | 1.5 | D. | 無法確定 |
分析 先利用垂直判斷出四邊形OECD是矩形,即可得出DE=OC=6,再用兩邊對應成比例夾角相等的兩三角形相似,得出△CHG∽△CDG,即:$\frac{GH}{DE}=\frac{CH}{CD}=\frac{1}{3}$,即可得出結論.
解答 解:如圖,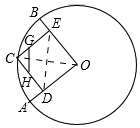 連接OC,DE,
連接OC,DE,
∵CD⊥OA,CE⊥OB,
∴∠CEO=∠CDO=90°,
∵半徑OA、OB互相垂直,
∴∠AOB=90°,
∴∠CEO=∠CDO=∠AOB=90°,
∴四邊形ODCE是矩形,
∴DE=OC=6,
∵CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,
∴$\frac{CG}{CE}=\frac{1}{3}$,$\frac{CH}{CD}=\frac{1}{3}$,
∴$\frac{CG}{CE}=\frac{CH}{CD}$=$\frac{1}{3}$,
∵∠HCG=∠DCE,
∴△CHG∽△CDG,
∴$\frac{GH}{DE}=\frac{CH}{CD}=\frac{1}{3}$,
∴GH=$\frac{1}{3}$DE=2,
故選B.
點評 此題是相似三角形的判定與性質,主要考查了矩形的判定和性質,解本題的關鍵是得出DE=OC=6,是一道很好的基礎題.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:初中數學 來源: 題型:填空題
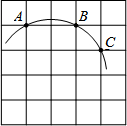 如圖,在5×5正方形網格中,一條圓弧經過A,B,C三點,已知點A的坐標是(-2,4),點C的坐標是(1,3),那么這條圓弧所在圓的圓心坐標是(-1,2).
如圖,在5×5正方形網格中,一條圓弧經過A,B,C三點,已知點A的坐標是(-2,4),點C的坐標是(1,3),那么這條圓弧所在圓的圓心坐標是(-1,2).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 第1天 | 第2天 | 第3天 | 第4天 | |
| 售價x(元/雙) | 150 | 200 | 250 | 300 |
| 銷售量y(雙) | 40 | 30 | 24 | 20 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
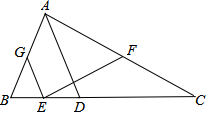 如圖,在△ABC中,點D在邊BC上,AB=AD,E是BD的中點,F是AC的中點.
如圖,在△ABC中,點D在邊BC上,AB=AD,E是BD的中點,F是AC的中點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
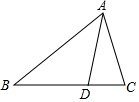 如圖,D是△ABC的邊BC上任一點,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面積為a,則△ACD的面積為( )
如圖,D是△ABC的邊BC上任一點,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面積為a,則△ACD的面積為( )| A. | a | B. | $\frac{1}{2}a$ | C. | $\frac{1}{3}a$ | D. | $\frac{1}{4}$a |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某校計劃修建一個長方形花壇,要求花壇的長與寬的比為2:1,如圖所示花壇中間為花卉種植區域,花卉種植區域前側留有2米寬的空地,其它三側各保留1米寬的通道,如果要求花卉種植區域的面積是55平方米,那么整個花壇的長與寬應為多少米?
某校計劃修建一個長方形花壇,要求花壇的長與寬的比為2:1,如圖所示花壇中間為花卉種植區域,花卉種植區域前側留有2米寬的空地,其它三側各保留1米寬的通道,如果要求花卉種植區域的面積是55平方米,那么整個花壇的長與寬應為多少米?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
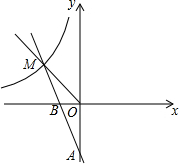 如圖,一次函數y=-2x-2的圖象分別交x軸、y軸于點B、A,與反比例函數y=$\frac{m}{x}$(m≠0)的圖象在第二象限交于點M,△OBM的面積是1.
如圖,一次函數y=-2x-2的圖象分別交x軸、y軸于點B、A,與反比例函數y=$\frac{m}{x}$(m≠0)的圖象在第二象限交于點M,△OBM的面積是1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com