
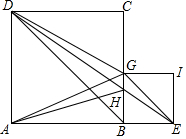
 已知正方形ABCD的面積是100,正方形BEFG的面積是25,點H是DE和BC的交點,求△GAH和△GHE的面積之和.
已知正方形ABCD的面積是100,正方形BEFG的面積是25,點H是DE和BC的交點,求△GAH和△GHE的面積之和. 分析 由AD∥CB,推出S△GAH=S△GDH,推出S△GAH+S△GHE=S△DGE,由BD∥EG,推出S△EGD=S△EGB=$\frac{1}{2}$•S正方形BEIG,由此即可解決問題.
解答 解: ∵四邊形ABCD是正方形,四邊形BEIG是正方形,
∵四邊形ABCD是正方形,四邊形BEIG是正方形,
∴∠DBG=∠BGE=45°,AD∥CB,
∴BD∥EG,
∴S△GAH=S△GDH,
∴S△GAH+S△GHE=S△DGE,
∵BD∥EG,
∴S△EGD=S△EGB=$\frac{1}{2}$•S正方形BEIG=$\frac{25}{2}$,
∴S△GAH+S△GHE=$\frac{25}{2}$.
點評 本題考查正方形的性質、平行線的性質等知識,解題的關鍵是記住平行線間的距離相等,學會利用平行線尋找面積相等的三角形,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (10-a)a | B. | a(10-a) | C. | 10(10-a)+a | D. | 10a+(10-a) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=-2x | B. | y=-2x+1 | C. | y=-$\frac{1}{2}$x-1 | D. | y=$\frac{1}{2}$x-1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
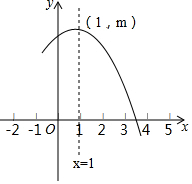 如圖是拋物線y=ax2+bx+c(a≠0)的部分圖象,其頂點坐標為(1,m),且與x軸的一個交點在點(3,0)和(4,0)之間,下列結論錯誤的是( )
如圖是拋物線y=ax2+bx+c(a≠0)的部分圖象,其頂點坐標為(1,m),且與x軸的一個交點在點(3,0)和(4,0)之間,下列結論錯誤的是( )| A. | a-b+c>0 | |
| B. | b2=4a(c-m) | |
| C. | 2a+c<0 | |
| D. | 一元二次方程ax2+bx+c=m-1有兩個不相等的實數根 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com