
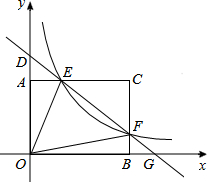
 如圖,矩形AOBC的頂點坐標分別為A(0,3),O(0,0),B(4,0),C(4,3),動點F在邊BC上(不與B,C重合),過點F的反比例函數y=$\frac{k}{x}$的圖象與邊AC交于點E,直線EF分別于y軸和x軸交于點D和G.給出下列命題:
如圖,矩形AOBC的頂點坐標分別為A(0,3),O(0,0),B(4,0),C(4,3),動點F在邊BC上(不與B,C重合),過點F的反比例函數y=$\frac{k}{x}$的圖象與邊AC交于點E,直線EF分別于y軸和x軸交于點D和G.給出下列命題:分析 (1)如答圖所示,若k=$\frac{21}{8}$,可證明直線EF是線段CN的垂直平分線,故命題②正確;
(2)若k=4,則計算S△OEF=$\frac{16}{3}$≠$\frac{8}{3}$,故命題①錯誤;
(3)因為點F不經過點C(4,3),所以k≠12,故命題③錯誤;
(4)求出直線EF的解析式,得到點D、G的坐標,然后求出線段DE、EG的長度;利用算式DE•EG=$\frac{25}{12}$,求出k=1,故命題④正確.
解答 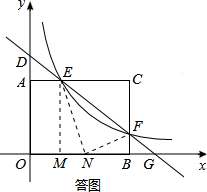 解:
解:
命題①正確.理由如下:
∵k=$\frac{21}{8}$,
∴E($\frac{7}{8}$,3),F(4,$\frac{21}{32}$),
∴CE=4-$\frac{7}{8}$=$\frac{25}{8}$,CF=3-$\frac{21}{32}$=$\frac{75}{32}$.
如答圖,過點E作EM⊥x軸于點M,則EM=3,OM=$\frac{7}{8}$;
在線段BM上取一點N,使得EN=CE=$\frac{25}{8}$,連接NF.
在Rt△EMN中,由勾股定理得:MN=$\sqrt{E{N}^{2}-E{M}^{2}}$=$\sqrt{(\frac{25}{8})^{2}-{3}^{2}}$=$\frac{7}{8}$,
∴BN=OB-OM-MN=4-$\frac{7}{8}$-$\frac{7}{8}$=$\frac{9}{4}$.
在Rt△BFN中,由勾股定理得:NF=$\sqrt{B{N}^{2}+B{F}^{2}}$=$\sqrt{(\frac{9}{4})^{2}+(\frac{21}{32})^{2}}$=$\frac{75}{32}$.
∴NF=CF,
又∵EN=CE,
∴直線EF為線段CN的垂直平分線,即點N與點C關于直線EF對稱,
故命題①正確;
命題②錯誤.理由如下:
∵k=4,
∴E($\frac{4}{3}$,3),F(4,1),
∴CE=4-$\frac{4}{3}$=$\frac{8}{3}$,CF=3-1=2.
∴S△OEF=S矩形AOBC-S△AOE-S△BOF-S△CEF=S矩形AOBC-$\frac{1}{2}$OA•AE-$\frac{1}{2}$OB•BF-$\frac{1}{2}$CE•CF=4×3-$\frac{1}{2}$×3×$\frac{4}{3}$-$\frac{1}{2}$×4×1-$\frac{1}{2}$×$\frac{8}{3}$×2=12-2-2-$\frac{8}{3}$=$\frac{16}{3}$,
∴S△OEF≠$\frac{8}{3}$,故命題②錯誤;
命題③錯誤.理由如下:
由題意,點F與點C(4,3)不重合,所以k≠4×3=12,故命題③錯誤;
命題④正確.理由如下:
為簡化計算,不妨設k=12m,則E(4m,3),F(4,3m).
設直線EF的解析式為y=ax+b,則有$\left\{\begin{array}{l}{4ma+b=3}\\{4a+b=3m}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{3}{4}}\\{b=3m+3}\end{array}\right.$,
∴y=-$\frac{3}{4}$x+3m+3.
令x=0,得y=3m+3,∴D(0,3m+3);
令y=0,得x=4m+4,∴G(4m+4,0).
如答圖,過點E作EM⊥x軸于點M,則OM=AE=4m,EM=3.
在Rt△ADE中,AD=OD-OA=3m,AE=4m,由勾股定理得:DE=5m;
在Rt△MEG中,MG=OG-OM=(4m+4)-4m=4,EM=3,由勾股定理得:EG=5.
∴DE•EG=5m×5=25m=$\frac{25}{12}$,解得m=$\frac{1}{12}$,
∴k=12m=1,故命題④正確.
綜上所述,正確的命題是:①④,
故答案為:①④.
點評 本題綜合考查了函數的圖象與性質、反比例函數圖象上點的坐標特征、比例系數k的幾何意義、待定系數法、矩形及勾股定理等多個知識點,有一定的難度.本題計算量較大,解題過程中注意認真計算.


 全能測控一本好卷系列答案
全能測控一本好卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com