
 某校王老師組織九(1)班同學開展數(shù)學活動,某天帶領(lǐng)同學們測量學校附近一電線桿的高.已知電線桿直立于地面上,在太陽光的照射下,電線桿的影子(折線BCD)恰好落在水平地面和斜坡上,在D處測得電線桿頂端A的仰角為30°,在C處測得電線桿頂端A的仰角為45°,斜坡與地面成60°角,CD=4m,請你根據(jù)這些數(shù)據(jù)求電線桿的高AB.(結(jié)果用根號表示)
某校王老師組織九(1)班同學開展數(shù)學活動,某天帶領(lǐng)同學們測量學校附近一電線桿的高.已知電線桿直立于地面上,在太陽光的照射下,電線桿的影子(折線BCD)恰好落在水平地面和斜坡上,在D處測得電線桿頂端A的仰角為30°,在C處測得電線桿頂端A的仰角為45°,斜坡與地面成60°角,CD=4m,請你根據(jù)這些數(shù)據(jù)求電線桿的高AB.(結(jié)果用根號表示) 分析 延長AD交BC的延長線于G,作DH⊥BG于H,根據(jù)正弦、余弦的定義求出CH、DH,根據(jù)正切的定義求出HG,設(shè)AB=xm,根據(jù)正切的定義求出BG,結(jié)合圖形列出方程,解方程即可.
解答 解:延長AD交BC的延長線于G,作DH⊥BG于H,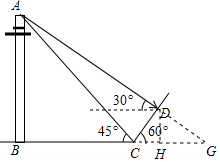
在Rt△DHC中,∠DCH=60°,CD=4,
則CH=CD•cos∠DCH=4×cos60°=2,
DH=CD•sin∠DCH=4×sin60°=$2\sqrt{3}$,
∵DH⊥BG,∠G=30°,
∴HG=$\frac{DH}{tan∠G}$=$\frac{{2\sqrt{3}}}{tan30°}$=6,
∴CG=CH+HG=2+6=8,
設(shè)AB=xm,
∵AB⊥BG,∠G=30°,∠BCA=45°,
∴BC=x,BG=$\frac{AB}{tan∠G}=\frac{x}{tan30°}$=$\sqrt{3}$x,
∵BG-BC=CG,
∴$\sqrt{3}$x-x=8,
解得:x=$\frac{8}{{\sqrt{3}-1}}$=4($\sqrt{3}$+1)(m)
答:電線桿的高為x=4($\sqrt{3}$+1)m.
點評 本題考查的是解直角三角形的應(yīng)用-仰角俯角問題,掌握仰角俯角的等腰、熟記銳角三角函數(shù)的定義是解題的關(guān)鍵.


科目:初中數(shù)學 來源: 題型:填空題
 如圖,O是正方形ABCD的中心,M是ABCD內(nèi)一點,∠DMC=90°,將△DMC繞O點旋轉(zhuǎn)180°后得到△NAB,若MD=3,CM=4,則MN的長為$\sqrt{2}$.
如圖,O是正方形ABCD的中心,M是ABCD內(nèi)一點,∠DMC=90°,將△DMC繞O點旋轉(zhuǎn)180°后得到△NAB,若MD=3,CM=4,則MN的長為$\sqrt{2}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | k>$\frac{1}{2}$ | B. | k<$\frac{1}{2}$ | C. | k=$\frac{1}{2}$ | D. | k≤$\frac{1}{2}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
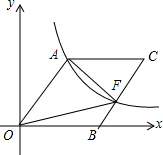 如圖,O為坐標原點,四邊形OACB是菱形,OB在x軸的正半軸上,反比例函數(shù)y=$\frac{48}{x}$在第一象限內(nèi)的圖象經(jīng)過點A(6,m),與BC交于點F,則△AOF的面積等于( )
如圖,O為坐標原點,四邊形OACB是菱形,OB在x軸的正半軸上,反比例函數(shù)y=$\frac{48}{x}$在第一象限內(nèi)的圖象經(jīng)過點A(6,m),與BC交于點F,則△AOF的面積等于( )| A. | 50 | B. | 40 | C. | 30 | D. | 20 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\sqrt{2}$>$\sqrt{3}$ | B. | 2<$\sqrt{5}$ | C. | 2$\sqrt{2}$<$\sqrt{5}$ | D. | 0<-$\sqrt{2}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
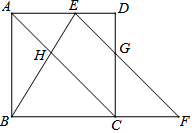 如圖,在正方形ABCD中,E是AD邊上的動點(與A、D不重合),點F在邊BC的延長線上,且AE=CF,連結(jié)EF與邊CD相交于點G,連結(jié)BE與對角線AC相交于點H.
如圖,在正方形ABCD中,E是AD邊上的動點(與A、D不重合),點F在邊BC的延長線上,且AE=CF,連結(jié)EF與邊CD相交于點G,連結(jié)BE與對角線AC相交于點H.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com