
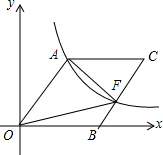
 如圖,O為坐標原點,四邊形OACB是菱形,OB在x軸的正半軸上,反比例函數y=$\frac{48}{x}$在第一象限內的圖象經過點A(6,m),與BC交于點F,則△AOF的面積等于( )
如圖,O為坐標原點,四邊形OACB是菱形,OB在x軸的正半軸上,反比例函數y=$\frac{48}{x}$在第一象限內的圖象經過點A(6,m),與BC交于點F,則△AOF的面積等于( )| A. | 50 | B. | 40 | C. | 30 | D. | 20 |
分析 連接AB,過點A作AD⊥x軸于點D,根據菱形的性質即可得出OA∥BC、OB=OA,由△AOF和△AOB有共同的底OA結合平行線的性質即可得出S△AOF=S△AOB,再根據點A的橫坐標結合反比例函數圖象上點的坐標特征即可得出點A的坐標,進而得出OB、AD的長度,利用三角形的面積公式即可求出S△AOB的值,此題得解.
解答 解:連接AB,過點A作AD⊥x軸于點D,如圖所示.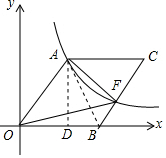
∵四邊形OACB是菱形,
∴OA∥BC,OB=OA,
又∵△AOF和△AOB有共同的底OA,
∴S△AOF=S△AOB.
∵反比例函數y=$\frac{48}{x}$在第一象限內的圖象經過點A(6,m),
∴6m=48,m=8,
∴OB=OA=$\sqrt{{6}^{2}+{8}^{2}}$=10,AD=8,
∴S△AOF=S△AOB=$\frac{1}{2}$OB•AD=$\frac{1}{2}$×10×8=40.
故選B.
點評 本題考查了反比例函數圖象上點的坐標特征、菱形的性質以及三角形的面積,根據面積法找出S△AOF=S△AOB是解題的關鍵.


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在Rt△ABC中,∠BAC=90°,AD⊥BC于點D,則下列結論不正確的是( )
如圖,在Rt△ABC中,∠BAC=90°,AD⊥BC于點D,則下列結論不正確的是( )| A. | cosC=$\frac{CD}{AC}$ | B. | cosC=$\frac{AC}{BC}$ | C. | cosC=$\frac{AD}{AC}$ | D. | cosC=$\frac{AD}{AB}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某校王老師組織九(1)班同學開展數學活動,某天帶領同學們測量學校附近一電線桿的高.已知電線桿直立于地面上,在太陽光的照射下,電線桿的影子(折線BCD)恰好落在水平地面和斜坡上,在D處測得電線桿頂端A的仰角為30°,在C處測得電線桿頂端A的仰角為45°,斜坡與地面成60°角,CD=4m,請你根據這些數據求電線桿的高AB.(結果用根號表示)
某校王老師組織九(1)班同學開展數學活動,某天帶領同學們測量學校附近一電線桿的高.已知電線桿直立于地面上,在太陽光的照射下,電線桿的影子(折線BCD)恰好落在水平地面和斜坡上,在D處測得電線桿頂端A的仰角為30°,在C處測得電線桿頂端A的仰角為45°,斜坡與地面成60°角,CD=4m,請你根據這些數據求電線桿的高AB.(結果用根號表示)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
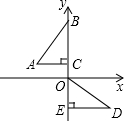 如圖,在平面直角坐標系中,點B、C、E在y軸上,Rt△ABC經過變換得到Rt△ODE,若點C的坐標為(0,1),AC=2,則這種變換可以是( )
如圖,在平面直角坐標系中,點B、C、E在y軸上,Rt△ABC經過變換得到Rt△ODE,若點C的坐標為(0,1),AC=2,則這種變換可以是( )| A. | △ABC繞點C逆時針旋轉90°,再向下平移1 | |
| B. | △ABC繞點C逆時針旋轉90°,再向下平移3 | |
| C. | △ABC繞點C順時針旋轉90°,再向下平移1 | |
| D. | △ABC繞點C順時針旋轉90°,再向下平移3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com