
分析 (1)整理成一般式后公式法求解可得;
(2)整理成一般式后公式法求解可得;
(3)將n看做已知數,利用公式法求解可得.
解答 解:(1)整理得:-x2+2$\sqrt{2}$x+4=0,
∵a=-1,b=2$\sqrt{2}$,c=4,
∴△=8-4×(-1)×4=24>0,
則x=$\frac{-2\sqrt{2}±2\sqrt{6}}{-2}$=$\sqrt{2}$$±\sqrt{6}$;
(2)整理得:3x2-6x+2=0,
∵a=3,b=-6,c=2,
∴△=36-4×3×2=12>0,
則x=$\frac{6±2\sqrt{3}}{6}$=$\frac{3±\sqrt{3}}{3}$;
(3)整理得4x2+6(n-1)x-9n=0,
∵a=4,b=6(n-1),c=-9n,
∴△=36(n-1)2+4×4×9n=36(n+1)2≥0,
則x=$\frac{-6(n-1)±6(n+1)}{8}$,
即x1=$\frac{3}{2}$,x2=-$\frac{3}{2}$n.
點評 本題主要考查解一元二次方程的能力,熟練掌握公式法是解題的關鍵


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:初中數學 來源: 題型:填空題
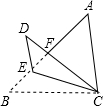 如圖,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4$\sqrt{2}$.
如圖,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com