
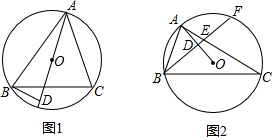
分析 (1)如圖1中,延長AD交⊙O于H,連接BH.首先證明∠ABD=∠H,由∠H=∠ACB即可證明.
(2)由(1)可知,∠ABD=∠ACB,由∠ABC=2∠ACB,推出∠FBC=∠C,推出$\widehat{FC}$=$\widehat{AB}$,推出$\widehat{BF}$=$\widehat{AC}$,推出BF=AC.
(3)如圖3中,連接AF、CF、AH.首先證明四邊形AFCH是平行四邊形,推出FG=GH=3,在Rt△AGF中,AG=$\sqrt{A{F}^{2}-F{G}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,設OA=OF=r,
在Rt△AOG中,由OA2=AG2+OG2,可得r2=42+(r-3)2,求出r即可解決問題.
解答 (1)證明:如圖1中,延長AD交⊙O于H,連接BH.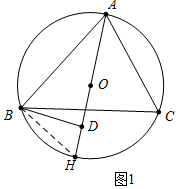
∵AB是直徑,
∴∠ABH=90°,
∴∠ABD+∠HBD=90°,
∵BD⊥AH,
∴∠BDH=90°,
∴∠H+∠HBD=90°,
∴∠H=∠ABD,
∵∠H=∠ACB,
∴∠ABD=∠ACB.
(2)證明:如圖2中,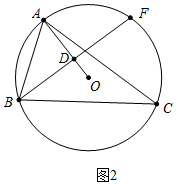
由(1)可知,∠ABD=∠ACB,
∵∠ABC=2∠ACB,
∴∠FBC=∠C,
∴$\widehat{FC}$=$\widehat{AB}$,
∴$\widehat{BF}$=$\widehat{AC}$,
∴BF=AC.
(3)解:如圖3中,連接AF、CF、AH.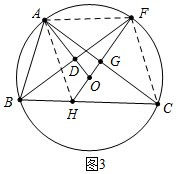
由(2)可知∠ABF=∠ACB=∠FBC=∠ACF,
∴$\widehat{AF}$=$\widehat{FC}$=$\widehat{AB}$,
∴AF=FC=AB=5,OF⊥AC,∠FAC=∠ACB,
∴AG=GC,AF∥CH,
在△AFG和△CHG中,
$\left\{\begin{array}{l}{∠FAG=∠HCG}\\{AG=GC}\\{∠AGF=∠CGH}\end{array}\right.$,
∴△AFG≌△CHG,
∴AF=CH,
∴四邊形AFCH是平行四邊形,
∴FG=GH=3,
在Rt△AGF中,AG=$\sqrt{A{F}^{2}-F{G}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,設OA=OF=r,
在Rt△AOG中,∵OA2=AG2+OG2,
∴r2=42+(r-3)2,
解得r=$\frac{25}{6}$,
∴OG=$\frac{7}{6}$,
∴OH=GH-OG=3-$\frac{7}{6}$=$\frac{11}{6}$.
點評 本題考查圓綜合題、圓周角定理、全等三角形的判定和性質、勾股定理、平行四邊形的判定和性質等知識,解題的關鍵是靈活運用所學知識,學會添加常用輔助線,構造特殊四邊形解決問題,屬于中考壓軸題.


 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖:已知直線y=x+1與坐標軸相交于點A,B;現把拋物線y=-x2的圖象平移,使它的圖象經過點A,B兩點,則平移的方法是( )
如圖:已知直線y=x+1與坐標軸相交于點A,B;現把拋物線y=-x2的圖象平移,使它的圖象經過點A,B兩點,則平移的方法是( )| A. | 向左平移一個單位 | B. | 向右平移一個單位 | ||
| C. | 向上平移一個單位 | D. | 向下平移一個單位 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
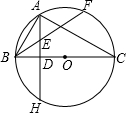 如圖,已知BC是⊙O的直徑,AH⊥BC,垂足為D,點A為$\widehat{BF}$的中點,BF交AD于點E,且BE•EF=32,AD=6
如圖,已知BC是⊙O的直徑,AH⊥BC,垂足為D,點A為$\widehat{BF}$的中點,BF交AD于點E,且BE•EF=32,AD=6查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 人長生不老 | |
| B. | 2016年奧運會中國隊獲100枚金牌 | |
| C. | 擲兩枚質地均勻的正方體骰子朝上一面的點數之積為21 | |
| D. | 一個星期為七天 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com