
 如圖,平面直角坐標系中,已知點P(2,2),C為y軸正半軸上一點,連接PC,線段PC繞點P順時針旋轉90°至線段PD,過點D作直線AB⊥x軸,垂足為B,直線AB與直線OP交于點A,且BD=4AD,直線CD與直線OP交于點Q,則點Q的坐標為($\frac{25}{6}$,$\frac{25}{6}$).
如圖,平面直角坐標系中,已知點P(2,2),C為y軸正半軸上一點,連接PC,線段PC繞點P順時針旋轉90°至線段PD,過點D作直線AB⊥x軸,垂足為B,直線AB與直線OP交于點A,且BD=4AD,直線CD與直線OP交于點Q,則點Q的坐標為($\frac{25}{6}$,$\frac{25}{6}$). 分析 過點P作PE⊥OC于E,EP的延長線交AB于F.首先證明△CPE≌△PDF,得到DF=PE=2,推出BD=BF+DF=4,由BD=4AD,推出AD=1,AB=OB=5,CE=PF=3,D(5,4),C(0,5),利用待定系數法求出直線CD的解析式,利用方程組即可求出點Q的坐標.
解答 解:過點P作PE⊥OC于E,EP的延長線交AB于F.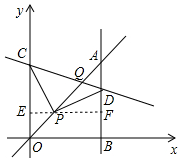
∵AB⊥OB,
∴∠OBF=∠EOB=∠FEO=90°,
∴四邊形EOBF是矩形,
∵P(2,2),
∴OE=PE=BF=2,
∵∠CPD=90°,
∴∠CPE+∠DPF=90°,∠ECP+∠CPE=90°,
∴∠ECP=∠DPF,
在△CPE和△PDF中,
$\left\{\begin{array}{l}{∠PEC=∠PFD}\\{∠PCE=∠DPF}\\{PC=PD}\end{array}\right.$,
∴△CPE≌△PDF,
∴DF=PE=2,
∴BD=BF+DF=4,
∵BD=4AD,
∴AD=1,AB=OB=5,
∴CE=PF=3,
∴D(5,4),C(0,5),
設直線CD的解析式為y=kx+b則有$\left\{\begin{array}{l}{b=5}\\{5k+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{5}}\\{b=5}\end{array}\right.$,
∴直線CD的解析式為y=-$\frac{1}{5}$x+5,
由$\left\{\begin{array}{l}{y=x}\\{y=-\frac{1}{5}x+5}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{25}{6}}\\{y=\frac{25}{6}}\end{array}\right.$,
∴點Q的坐標為($\frac{25}{6}$,$\frac{25}{6}$).
故答案為($\frac{25}{6}$,$\frac{25}{6}$).
點評 本題考查一次函數的應用、待定系數法、全等三角形的判定和性質、二元一次方程組等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形解決問題,學會構建一次函數,利用方程組求交點坐標,屬于中考填空題中的壓軸題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
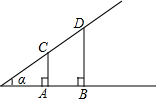 如圖,A,B,C,D分別是∠α邊上的四個點,且CA,DB均垂直于∠α的一條邊,如果CA=AB=2,BD=3,那么tanα=$\frac{1}{2}$.
如圖,A,B,C,D分別是∠α邊上的四個點,且CA,DB均垂直于∠α的一條邊,如果CA=AB=2,BD=3,那么tanα=$\frac{1}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
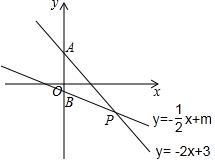 如圖,函數y=-2x+3與y=-$\frac{1}{2}$x+m的圖象交于P(n,-2).
如圖,函數y=-2x+3與y=-$\frac{1}{2}$x+m的圖象交于P(n,-2).查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x$<\frac{1}{2}$ | B. | x$>\frac{1}{2}$ | C. | x$<-\frac{1}{2}$ | D. | x$>-\frac{1}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
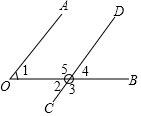 如圖,直線CD與∠AOB的邊OB相交.
如圖,直線CD與∠AOB的邊OB相交.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com