
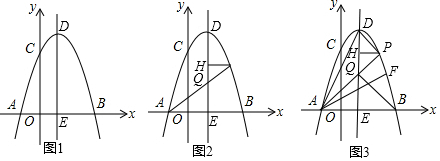
分析 (1)根據(jù)定點(diǎn)的坐標(biāo)等于DE,可得關(guān)于k的方程,根據(jù)解方程,可得答案;
(2)根據(jù)對(duì)稱軸公式,可得D點(diǎn)坐標(biāo);根據(jù)矩形的判定與性質(zhì),可得PH與KE的關(guān)系,根據(jù)同一個(gè)角的正切值,可得QE,根據(jù)線段的和差,可得答案;
(3)根據(jù)自變量與函數(shù)值的對(duì)應(yīng)關(guān)系,可得A,B點(diǎn)坐標(biāo),根據(jù)平行線的性質(zhì),可得∠PDH=∠BQE,根據(jù)等角的正切值相等,可得m的值,根據(jù)全等三角形的判定與性質(zhì),可得DP與PM的關(guān)系,根據(jù)終點(diǎn)坐標(biāo),可得M的坐標(biāo),根據(jù)待定系數(shù)法,可得AM,跟解方程組,可得答案.
解答 解:(1)∵D為拋物線的頂點(diǎn),DE=4,
∴$\frac{4×(-1)k-(k-1)^{2}}{4×(-1)}$=4,
解得k1=3,k2=-5(舍),
∴拋物線的解析式y(tǒng)=-x2+2x+3;
(2)解:對(duì)稱軸為x=-$\frac{2}{2×(-1)}$=1,
∴頂點(diǎn)坐標(biāo)為(1,4),
設(shè)P[1+m,-(1+m2)+2(1+m)+3],
如圖1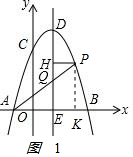 ,過P作PK⊥x軸于點(diǎn)K,
,過P作PK⊥x軸于點(diǎn)K,
∵對(duì)稱軸與x軸交于E點(diǎn),
∴DE⊥x軸,又∵PH⊥DE,
∴∠DEB=∠PKO=∠PHQ=90°,
∴四邊形PHEK是矩形,
∴PH=KE=m,
∵tan∠PAK=$\frac{PK}{AK}$=$\frac{QE}{AE}$,
∴$\frac{-(1+m)^{2}+2(1+m)+3}{(1+m)-(-1)}$=$\frac{QE}{1-(-1)}$
∴QE=-2m+4,
∴d=DQ=DE-QE=4-(-2m+4)=2m;
(3)解:當(dāng)y=0時(shí),-x2+2x+3=0,
解得x1=-1,x2=3,
∴A(-1,0),B(3,0).
∵DP∥BQ,
∴∠PDH=∠BQE,
tan∠PDH=tan∠BQE,$\frac{PH}{DH}$=$\frac{BE}{QE}$,
∴$\frac{m}{4-[-(1+m)^{2}+2(1+m)+3}$=$\frac{2}{-2m+4}$,
∴m1=0舍),m2=1,P(2,3).
由勾股定理,得
AD=2$\sqrt{5}$,DP=$\sqrt{2}$,PA=3$\sqrt{2}$.
∵AD2=DP2+AP2,
∴∠APD=90°.
如圖2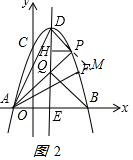 ,延長(zhǎng)DP交射線AF于點(diǎn)M,
,延長(zhǎng)DP交射線AF于點(diǎn)M,
在△ADP和△AMP中,
$\left\{\begin{array}{l}{∠DAP=∠MAP}\\{AP=AP}\\{∠ADP=∠AMP}\end{array}\right.$,
∴△ADP≌△AMP(ASA),
∴PD=PM.
∵D(1,4),P(2,3),
∴M(3,2).
由A,M點(diǎn),得
AM的解析式為y=$\frac{1}{2}$x+$\frac{1}{2}$
聯(lián)立AM與拋物線,得
$\left\{\begin{array}{l}{y=\frac{1}{2}x+\frac{1}{2}}\\{y=-{x}^{2}+2x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=\frac{5}{2}}\\{{y}_{1}=\frac{7}{4}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=0}\end{array}\right.$(舍),
F點(diǎn)的坐標(biāo)為($\frac{5}{2}$,$\frac{7}{4}$).
點(diǎn)評(píng) 本題考查了二次函數(shù)綜合題,(1)利用DE的長(zhǎng)得出k值是求函數(shù)解析式的關(guān)鍵;(2)利用了矩形的判定與性質(zhì),利用正切值相等得出QE是解題關(guān)鍵;(3)利用全等三角形的判定與性質(zhì)得出PD=PM是解題關(guān)鍵,又利用方程組得出拋物線與直線的交點(diǎn)坐標(biāo).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | (2,0) | B. | (2.5,0) | C. | (4,0) | D. | (4.5,0) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | a=5,b=-6 | B. | a=5,b=6 | C. | a=1,b=6 | D. | a=1,b=-6 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
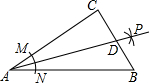 如圖,在Rt△ABC中,∠C=90°,以頂點(diǎn)A為圓心,適當(dāng)長(zhǎng)為半徑畫弧,分別交AC,AB于點(diǎn)M、N,再分別以點(diǎn)M、N為圓心,大于$\frac{1}{2}$MN的長(zhǎng)為半徑畫弧,兩弧交于點(diǎn)P,作射線AB交邊BC于點(diǎn)D,若CD=4,AB=15,則△ABD的面積是30.
如圖,在Rt△ABC中,∠C=90°,以頂點(diǎn)A為圓心,適當(dāng)長(zhǎng)為半徑畫弧,分別交AC,AB于點(diǎn)M、N,再分別以點(diǎn)M、N為圓心,大于$\frac{1}{2}$MN的長(zhǎng)為半徑畫弧,兩弧交于點(diǎn)P,作射線AB交邊BC于點(diǎn)D,若CD=4,AB=15,則△ABD的面積是30.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 甲市 | 5 | 15 | 20 | 20 | 60 | 140 | 185 | 200 | 60 | 35 | 15 | 10 |
| 乙市 | 25 | 40 | 55 | 140 | 300 | 430 | 310 | 410 | 320 | 120 | 35 | 25 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com