
 如圖,四邊形ABCD內接于圓,延長AD、BC相交于點E,點F是BD的延長線上的點,且AB=AC.
如圖,四邊形ABCD內接于圓,延長AD、BC相交于點E,點F是BD的延長線上的點,且AB=AC.分析 (1)由∠ABC+∠ADC=180°,∠CDE+∠ADC=180°,推出∠CDE=∠ABC,由∠EDF=∠ADB=∠ACB,以及AB=AC,推出∠ABC=∠ACB,即可推出∠EDF=∠CDE解決問題.
(2)證△ABD∽△AEB,通過相似三角形的對應成比例線段,求出DE的值.
解答 (1)證明:∵∠ABC+∠ADC=180°,∠CDE+∠ADC=180°,
∴∠CDE=∠ABC,
∵∠EDF=∠ADB=∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EDF=∠CDE,
∴DE平分∠CDF.
(2)解:∵∠ADB=∠ABC,∠DAB=∠BAE,
∴△ABD∽△AEB
∴$\frac{AB}{AE}$=$\frac{AD}{AB}$,
∵AB=AC=3,AD=2
∴AE=$\frac{A{B}^{2}}{AD}$=$\frac{9}{2}$,
∴DE=$\frac{9}{2}$-2=$\frac{5}{2}$(cm).
點評 本題綜合考查了角平分線的判定,相似三角形的判定和性質,圓內接四邊形的性質等知識,解題的關鍵是靈活運用所學知識,學會正確尋找相似三角形解決問題,屬于中考常考題型..


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
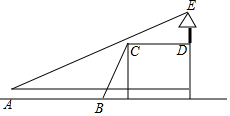 如圖,小周站在A處,他的對面有一斜坡BC(坡度i=12:5),現測得小周所站A處到斜坡底端B的距離,AB=15米,坡面BC長為13米.在斜坡頂端C不遠處D有一棵樹,測得CD=10米,小周看樹的頂部E的仰角為30°,此時小周眼睛到地面的高度為1.8米,則數的高度DE約為( )(精確到1米,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)
如圖,小周站在A處,他的對面有一斜坡BC(坡度i=12:5),現測得小周所站A處到斜坡底端B的距離,AB=15米,坡面BC長為13米.在斜坡頂端C不遠處D有一棵樹,測得CD=10米,小周看樹的頂部E的仰角為30°,此時小周眼睛到地面的高度為1.8米,則數的高度DE約為( )(精確到1米,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)| A. | 5 | B. | 7 | C. | 12 | D. | 17 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
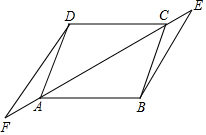 如圖,?ABCD中,E,F是直線AC上兩點,請在題目中添加合適的條件,就可以證明:BE=DF.
如圖,?ABCD中,E,F是直線AC上兩點,請在題目中添加合適的條件,就可以證明:BE=DF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
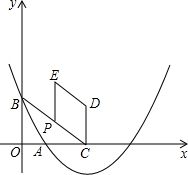 如圖在平面直角坐標系xOy中,拋物線y=$\frac{\sqrt{3}}{5}{x}^{2}$+bx+c過點A(1,0),B(0,$\sqrt{3}$),這條拋物線的對稱軸與x軸交于點C,點P為射線CB上一個動點(不與點C重合),射線PC繞點P逆時針旋轉120°,得線段PE,作平行四邊形PCDE.
如圖在平面直角坐標系xOy中,拋物線y=$\frac{\sqrt{3}}{5}{x}^{2}$+bx+c過點A(1,0),B(0,$\sqrt{3}$),這條拋物線的對稱軸與x軸交于點C,點P為射線CB上一個動點(不與點C重合),射線PC繞點P逆時針旋轉120°,得線段PE,作平行四邊形PCDE.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com