
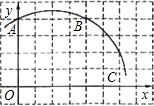
 如圖,已知直角坐標系中一條圓弧經過正方形網格的格點A、B、C.
如圖,已知直角坐標系中一條圓弧經過正方形網格的格點A、B、C.分析 (1)作AB和BC的垂直平分線,兩線交于一點M,點M即為所求,由圖形可知:這點的坐標是(2,0);
(2)設過C點與x軸垂直的直線與x軸的交點為E,連結MC,作直線CD.得出CE=2,ME=4,ED=1,MD=5,根據勾股定理求出MC2=20,CD2=5,推出∠MCD=90°,根據切線的判定推出即可.
解答 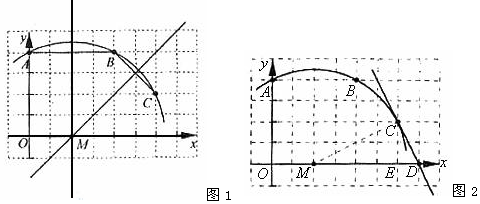 解:(1)如圖1,連接AB、BC,
解:(1)如圖1,連接AB、BC,
作AB和BC的垂直平分線,兩線交于一點M,點M即為所求,
由圖形可知:這點的坐標是(2,0),
∴圓弧所在圓的圓心M點的坐標是(2,0);
(2)由A(0,4),可得小正方形的邊長為1,從而可得B(4,4)、C(6,2),
如圖2,設過C點與x軸垂直的直線與x軸的交點為E,連結MC,作直線CD.
∴CE=2,ME=4,ED=1,MD=5,
在Rt△CEM中,∠CEM=90°,
∴MC2=ME2+CE2=42+22=20,
在Rt△CED中,∠CED=90°,
∴CD2=ED2+CE2=12+22=5,
∴MD2=MC2+CD2,
∴∠MCE=90°,
∵MC為半徑,
∴直線CD是⊙M的切線.
點評 本題考查了勾股定理,切線的判定等,在判定一條直線為圓的切線時,當已知條件中未明確指出直線和圓是否有公共點時,常過圓心作該直線的垂線段,證明該線段的長等于半徑;當已知條件中明確指出直線與圓有公共點時,常連接過該公共點的半徑,證明該半徑垂直于這條直線.


科目:初中數學 來源: 題型:填空題
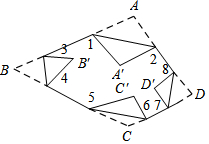 如圖所示,把一個四邊形紙片ABCD的四個頂角分別向內折疊,折疊之后,4個頂點不重合,那么圖中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度數是720°.
如圖所示,把一個四邊形紙片ABCD的四個頂角分別向內折疊,折疊之后,4個頂點不重合,那么圖中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度數是720°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| x | 6.1 | 6.2 | 6.3 | 6.4 |
| y=ax2+bx+c | -0.3 | -0.1 | 0.2 | 0.4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在如圖所示的平面直角坐標系中表示下面各點:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).
在如圖所示的平面直角坐標系中表示下面各點:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com