
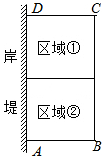
 為了節省材料,某水產養殖戶利用水庫的岸堤為一邊,用總長為a米(a為大于21的常數)的圍網在水庫中圍成了如圖所示的①②兩塊矩形區域.已知岸堤的可用長度不超過21米.設AB的長為x米,矩形區域ABCD的面積為y平方米
為了節省材料,某水產養殖戶利用水庫的岸堤為一邊,用總長為a米(a為大于21的常數)的圍網在水庫中圍成了如圖所示的①②兩塊矩形區域.已知岸堤的可用長度不超過21米.設AB的長為x米,矩形區域ABCD的面積為y平方米分析 (1)設AB的長為x米,則BC的長為(a-3x)米,根據矩形民機公式可得函數解析式,由0<BC≤21可得x的范圍;
(2)將a=30代入解析式配方成頂點式,結合x的范圍可得最值;
(3)將a=48代入解析式配方成頂點式,結合x的范圍可得最值.
解答 解:(1)設AB的長為x米,則BC的長為(a-3x)米,
根據題意得:y=x(a-3x)=-3x2+ax,
由a-3x≤21可得x≥$\frac{a-21}{3}$,
由a-3x>0得x<$\frac{a}{3}$,
∴$\frac{a-21}{3}$≤x<$\frac{a}{3}$;
(2)當a=30時,y=-3x2+30x=-3(x-5)2+75,
∵3≤x<10,
∴當x=5時,y取得最大值為75;
(3)當a=48時,y=-3x2+48x=-3(x-8)2+192,
∴當x=8時,y取得最大值為192.
點評 本題主要考查二次函數的應用,根據矩形面積公式得出函數解析式,利用二次函數的頂點式,結合二次函數的性質得出其最值情況是解題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
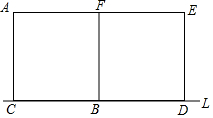 如圖,已知邊長等于8個單位長度的兩個完全相同的正方形ACBF、BDEF有公共邊BF,且CB與BD均在直線L上,將正方形ACBF沿直線L以1單位/秒向右平移,設移動時間為t秒,正方形ACBF在移動過程中與正方形BDEF重疊的面積為S,試求:
如圖,已知邊長等于8個單位長度的兩個完全相同的正方形ACBF、BDEF有公共邊BF,且CB與BD均在直線L上,將正方形ACBF沿直線L以1單位/秒向右平移,設移動時間為t秒,正方形ACBF在移動過程中與正方形BDEF重疊的面積為S,試求:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com