
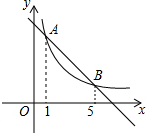
 如圖,直線y=k1x+b與雙曲線y=$\frac{{k}_{2}}{x}$交于A、B兩點,其橫坐標分別為1和5,則不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
如圖,直線y=k1x+b與雙曲線y=$\frac{{k}_{2}}{x}$交于A、B兩點,其橫坐標分別為1和5,則不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )| A. | -5<x<-1或x>0 | B. | 0<x<1或x>5 | C. | 1<x<5 | D. | -5<x<-1 |
分析 根據不等式與直線和雙曲線解析式的關系,相當于把直線向下平移2b個單位,然后根據函數的對稱性可得交點坐標與原直線的交點坐標關于原點對稱,再找出直線在雙曲線下方的自變量x的取值范圍即可.
解答 解:由k1x<$\frac{{k}_{2}}{x}$+b,得,k1x-b<$\frac{{k}_{2}}{x}$,
所以,不等式的解集可由雙曲線不動,直線向下平移2b個單位得到,
直線向下平移2b個單位的圖象如圖所示,交點A′的橫坐標為-1,交點B′的橫坐標為-5,
當-5<x<-1或x>0時,雙曲線圖象在直線圖象上方,
所以,不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是-5<x<-1或x>0.
故選A.
點評 本題主要考查了反比例函數與一次函數的交點問題,根據不等式與函數解析式得出不等式的解集與雙曲線和向下平移2b個單位的直線的交點有關是解題的關鍵.


科目:初中數學 來源: 題型:解答題
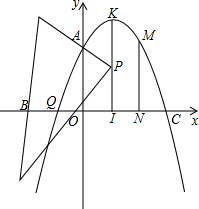 如圖,已知拋物線y=ax2+bx+3經過點B(-1,0)、C(3,0),交y軸于點A,
如圖,已知拋物線y=ax2+bx+3經過點B(-1,0)、C(3,0),交y軸于點A,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在平面直角坐標系xOy中,定義直線y=ax+b為拋物線y=ax2+bx的特征直線,C(a,b)為其特征點.設拋物線y=ax2+bx與其特征直線交于A、B兩點(點A在點B的左側).
在平面直角坐標系xOy中,定義直線y=ax+b為拋物線y=ax2+bx的特征直線,C(a,b)為其特征點.設拋物線y=ax2+bx與其特征直線交于A、B兩點(點A在點B的左側).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在菱形ABCD中,對角線BD=6,∠BAD=60°,則對角線AC的長等于( )
如圖,在菱形ABCD中,對角線BD=6,∠BAD=60°,則對角線AC的長等于( )| A. | 12 | B. | $3\sqrt{3}$ | C. | 6 | D. | $6\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,小明想測量院子里一棵樹的高度,在某一時刻,他站在該樹的影子上,前后移動,直到他本身的影子的頂端正好與樹影的頂端重疊.此時,他與該樹的水平距離2m,小明身高1.5m,他的影長是1.2m,那么該樹的高度為4m.
如圖,小明想測量院子里一棵樹的高度,在某一時刻,他站在該樹的影子上,前后移動,直到他本身的影子的頂端正好與樹影的頂端重疊.此時,他與該樹的水平距離2m,小明身高1.5m,他的影長是1.2m,那么該樹的高度為4m.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
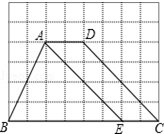 如圖,方格紙中每個小正方形的邊長均為1,四邊形ABCD的四個頂點都在小正方形的頂點上,點E在BC邊上,且點E在小正方形的頂點上,連接AE.
如圖,方格紙中每個小正方形的邊長均為1,四邊形ABCD的四個頂點都在小正方形的頂點上,點E在BC邊上,且點E在小正方形的頂點上,連接AE.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3×105 | B. | 3×106 | C. | 3×104 | D. | 30×105 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com