
 在平面直角坐標系xOy中,定義直線y=ax+b為拋物線y=ax2+bx的特征直線,C(a,b)為其特征點.設拋物線y=ax2+bx與其特征直線交于A、B兩點(點A在點B的左側).
在平面直角坐標系xOy中,定義直線y=ax+b為拋物線y=ax2+bx的特征直線,C(a,b)為其特征點.設拋物線y=ax2+bx與其特征直線交于A、B兩點(點A在點B的左側).分析 (1)根據點A、B求出直線解析式,得到a、b值,即可寫出點C坐標;
(2)聯(lián)立直線與拋物線解析式,即可求出點A(1,a+b),B(-$\frac{b}{a}$,0),根據圖象描出兩點即可;
(3)求出點D坐標,根據點F、C、E坐標及平行四邊形性質,即可求出特征點C的坐標,根據已知和已證得:C(a,b),E(0,b),F(xiàn)(1,0),D(-$\frac{b}{2a}$,0),由CEDF平行四邊形性質可以得出b關于a的函數關系式,利用已知$\frac{1}{2}$<tan∠ODE<2求出a的取值范圍,進而求出b的取值范圍;
解答 解:(1)∵A(0,0),B(1.3),
代入:直線y=ax+b,
解得:a=3,b=0,
∴直線y=3x,拋物線解析式:y=3x2,
∴C(3,0).
故答案為:(3,0);
(2)聯(lián)立直線y=ax+b與拋物線y=ax2+bx,
得:ax2+(b-a)x-b=0,
∴(ax+b)(x-1)=0,
解得:x=-$\frac{b}{a}$,x=1,
∴A(1,a+b),B(-$\frac{b}{a}$,0).
點A、點B的位置如圖所示;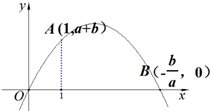
(3)①如圖,
∵特征點C為直線y=-4x上一點,
∴b=-4a.
∵拋物線y=ax2+bx的對稱軸與x軸交于點D,
∴對稱軸$x=-\frac{b}{2a}=2$.
∴點D的坐標為(2,0).
∵點F的坐標為(1,0),
∴DF=1.
∵特征直線y=ax+b交y軸于點E,
∴點E的坐標為(0,b).
∵點C的坐標為(a,b),
∴CE∥DF.
∵DE∥CF,
∴四邊形DECF為平行四邊形.
∴CE=DF=1.
∴a=-1.
∴特征點C的坐標為(-1,4).
②由已知和已證得:
C(a,b),E(0,b),F(xiàn)(1,0),D(-$\frac{b}{2a}$,0),
∵$\frac{1}{2}$<tan∠ODE<2,
∴$\frac{1}{2}$<$\frac{OE}{OD}$<2,
∴$\frac{1}{2}$<|$\frac{b}{-\frac{b}{2a}}$|<2,
解得:$\frac{1}{2}$<|2a|<2,
∴-1<a<-$\frac{1}{4}$或$\frac{1}{4}$<a<1,
∵DE∥CF,CE∥DF,
∴CE=DF,
由題意可得:1+$\frac{b}{2a}$=a,(可以畫出三種圖象,由此得出這個結論)
整理得:b=2a2-2a
即:b=2(a-$\frac{1}{2}$)2-$\frac{1}{2}$
當b=2(a-$\frac{1}{2}$)2-$\frac{1}{2}$時,
當-1<a<-$\frac{1}{4}$,可得$\frac{5}{8}<b<4$.
當$\frac{1}{4}$<a<1時,可得-$\frac{1}{2}$≤b<0
綜上所述:$\frac{5}{8}<b<4$或-$\frac{1}{2}$≤b<0.
點評 題目考查了新定義特征點、特征線及二次函數綜合應用,題目整體難易適中,對學生最大的難點在于對新定義的理解.適合學生對中考壓軸題目訓練.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
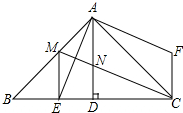 如圖,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于點E,在△ABC外有一點F,使FA⊥AE,F(xiàn)C⊥BC.
如圖,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于點E,在△ABC外有一點F,使FA⊥AE,F(xiàn)C⊥BC.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
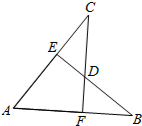 如圖,AB=AC,CF⊥AB于F,BE⊥AC于E,CF與BE交于點D.有下列結論:①△ABE≌△ACF;②△BDF≌△CDE;③點D在∠BAC的平分線上;④點C在AB的中垂線上.以上結論錯誤的有( )個.
如圖,AB=AC,CF⊥AB于F,BE⊥AC于E,CF與BE交于點D.有下列結論:①△ABE≌△ACF;②△BDF≌△CDE;③點D在∠BAC的平分線上;④點C在AB的中垂線上.以上結論錯誤的有( )個.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
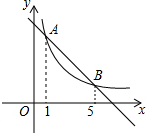 如圖,直線y=k1x+b與雙曲線y=$\frac{{k}_{2}}{x}$交于A、B兩點,其橫坐標分別為1和5,則不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
如圖,直線y=k1x+b與雙曲線y=$\frac{{k}_{2}}{x}$交于A、B兩點,其橫坐標分別為1和5,則不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )| A. | -5<x<-1或x>0 | B. | 0<x<1或x>5 | C. | 1<x<5 | D. | -5<x<-1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 24個交點 | B. | 36個交點 | C. | 45個交點 | D. | 55個交點 |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com