

| A. | 16cm | B. | 12cm | C. | 9cm | D. | 6$\sqrt{2}$cm |
分析 根據翻折的對稱性可知EG垂直平分FH,點K為F與EG中點連線的中點,然后根據HK的長度求出HF,即為正方形ABCD的邊長,從而得解.
解答 解:∵正方形ABCD無縫隙無重疊得到四邊形EFGH,
∴EG垂直平分FH,
∵四邊形EFGH的一個角向內折起點F恰好和EG的中點重合,
∴點K為F與EG中點連線的中點,
∵HK=12cm,
∴HF=HK÷$\frac{3}{4}$=9÷$\frac{3}{4}$=12cm,
∴正方形ABCD的邊長為12cm,
∴AB=12cm.
故選B.
點評 本題考查了翻折變換的性質,根據翻折前后的兩個圖形能夠互相重合判斷出垂直平分和中點,最后求出HF的長是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | x-4 | B. | x+3 | C. | $\frac{1}{x-3}$ | D. | $\frac{1}{x+3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (-3,-4) | B. | (-3,4) | C. | (2,-6) | D. | ($\frac{\sqrt{2}}{2}$,-12$\sqrt{2}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
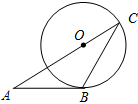 如圖,AB與⊙O目切于點B,連接AO,AO的延長線交⊙O于點C,連接BC,若∠A=40°,則∠C的度數為( )
如圖,AB與⊙O目切于點B,連接AO,AO的延長線交⊙O于點C,連接BC,若∠A=40°,則∠C的度數為( )| A. | 50° | B. | 25° | C. | 20° | D. | 15° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 已知實數m、n在數軸上的對應點的位置如圖,則|m-n|+$\sqrt{1-2n+{n}^{2}}$=( )
已知實數m、n在數軸上的對應點的位置如圖,則|m-n|+$\sqrt{1-2n+{n}^{2}}$=( )| A. | m-1 | B. | m+1 | C. | 2n-m+1 | D. | 2n-m-1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com