
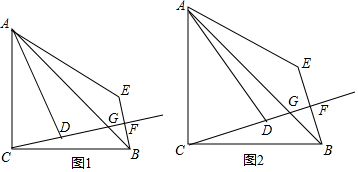
分析 (1)過A作AM⊥CD于M.只要證明△ACM≌△CBF,推出CM=BF,由CD=2CM,BE=2BF,即可推出CD=BE.
(2)延長CF到N,使得FN=CM,由△ACM≌△CBF,推出AM=CF,BF=CM=DM=FN,設FN=BF=a,AM=b,由CM=FN,推出MN=AM=b,FG=DG=$\frac{1}{2}$(b-2a),GM=DM+DG=$\frac{b}{2}$,由BF∥AM,推出$\frac{BF}{AM}$=$\frac{GF}{GM}$=$\frac{BG}{AG}$,可得$\frac{a}{b}$=$\frac{\frac{1}{2}(b-2a)}{\frac{1}{2}b}$,推出b=3a,由此即可解決問題.
(3)連接CE、在線段CF上取一點M,使得CM=BM,連接BM.首先證明△ACE是等邊三角形,推出AE=CE=BC,設BE=2a,則BF=a,想辦法求出BC即可解決問題.
解答 (1)證明:過A作AM⊥CD于M.
∵AC=AD,AM⊥CD,
∴CM=DM,∠ACB=∠AMC=90°,
∴∠ACM+∠BCF=90°,
∵點B關于射線CD的對稱點為E,
∴CF⊥EB,EF=FB,
∴∠CFB=90°,
∴∠BCF+∠CBF=90°,
∴∠ACM=∠CBF,
在△ACM和△CBF中,
$\left\{\begin{array}{l}{∠AMC=∠CFB}\\{∠ACM=∠CBF}\\{AC=CB}\end{array}\right.$,
∴△ACM≌△CBF,
∴CM=BF,
∵CD=2CM,BE=2BF,
∴CD=BE.
(2)解:延長CF到N,使得FN=CM,
由(1)可知,△ACM≌△CBF,
∴AM=CF,BF=CM=DM=FN,設FN=BF=a,AM=b,
∵CM=FN,
∴MN=AM=b,FG=DG=$\frac{1}{2}$(b-2a),GM=DM+DG=$\frac{b}{2}$,
∵BF∥AM,
∴$\frac{BF}{AM}$=$\frac{GF}{GM}$=$\frac{BG}{AG}$,
∴$\frac{a}{b}$=$\frac{\frac{1}{2}(b-2a)}{\frac{1}{2}b}$,
∴b=3a,
∴$\frac{BG}{AG}$=$\frac{a}{3a}$=$\frac{1}{3}$,
∴$\frac{AG}{BG}$=3.
(3)解:連接CE、在線段CF上取一點M,使得CM=BM,連接BM.
∵∠CAD=30°,AC=AD,
∴∠ACD=75°,∵∠ACB=90°,
∴∠BCF=∠ECF=15°,
∴∠BCE=30°,
∴∠ACE=60°,
∵CB=CE=CA,
∴△ACE是等邊三角形,
∴AE=CE=BC,設BE=2a,則BF=a,
在Rt△BMF中,∵∠BMF=∠MCB+∠MBC=30°,
∴CM=BM=2a,MF=$\sqrt{3}$a,
∴BC=$\sqrt{B{F}^{2}+C{F}^{2}}$=$\sqrt{{a}^{2}+(2a+\sqrt{3}a)^{2}}$=($\sqrt{6}$+$\sqrt{2}$)a,
∴$\frac{AE}{BE}$=$\frac{(\sqrt{6}+\sqrt{2})a}{2a}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
點評 本題考查三角形綜合題、等腰直角三角形的性質、全等三角形的判定和性質、等邊三角形的判定和性質、平行線分線段成比例定理等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形,學會利用參數構建方程,學會用轉化的首先思考問題,屬于中考壓軸題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y2<y3<y1 | D. | y3<y2<y1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 有最大值-23 | B. | 有最小值-23 | C. | 有最大值23 | D. | 有最小值23 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
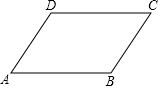 如圖,在?ABCD中,下列等式成立的是( )
如圖,在?ABCD中,下列等式成立的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$+$\overrightarrow{BD}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ | C. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$+$\overrightarrow{BD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
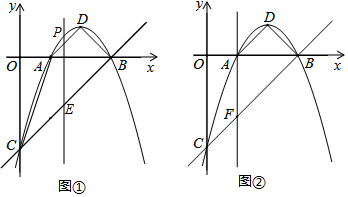
 某青少年科技創新小組設計了一個遙控車沿直線軌道AC做勻速直線運動的模型.甲、乙兩遙控車同時分別從A,B兩處出發,沿軌道到達C處,設t(分)后甲、乙兩遙控車與B處的距離分別為d1,d2,則d1,d2與t的函數關系如圖所示,試根據圖象解決下列問題:
某青少年科技創新小組設計了一個遙控車沿直線軌道AC做勻速直線運動的模型.甲、乙兩遙控車同時分別從A,B兩處出發,沿軌道到達C處,設t(分)后甲、乙兩遙控車與B處的距離分別為d1,d2,則d1,d2與t的函數關系如圖所示,試根據圖象解決下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com