
分析 (1)觀察知,找第一個等號后面的式子規律是關鍵:分子不變,為1;分母是兩個連續奇數的乘積,它們與式子序號之間的關系為:序號的2倍減1和序號的2倍加1.
(2)運用(1)中變化規律計算得出即可.
(3)運用以上規律裂項求和即可.
解答 解:(1)觀察下列等式:
第1個等式:a1=$\frac{1}{1×3}$=$\frac{1}{2}$(1-$\frac{1}{3}$)
第2個等式:a2=$\frac{1}{3×5}$=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)
第3個等式:a3=$\frac{1}{5×7}$=$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$)
第4個等式:a4=$\frac{1}{7×9}$=$\frac{1}{2}$($\frac{1}{7}$-$\frac{1}{9}$)
…
則第5個等式:a5=$\frac{1}{9×11}$=$\frac{1}{2}$×($\frac{1}{9}$-$\frac{1}{11}$);
故答案為$\frac{1}{9×11}$,$\frac{1}{2}$×($\frac{1}{9}$-$\frac{1}{11}$);
(2)由(1)知,an=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
故答案為:$\frac{1}{(2n-1)(2n+1)}$,$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$);
(3)原式=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{99×101}$
=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$)+…+$\frac{1}{2}$($\frac{1}{99}$-$\frac{1}{101}$)
=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{99}$-$\frac{1}{101}$)
=$\frac{1}{2}$×$\frac{100}{101}$
=$\frac{50}{101}$.
點評 此題考查了數字的規律及運用規律計算.尋找規律大致可分為2個步驟:不變的和變化的;變化的部分與序號的關系.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
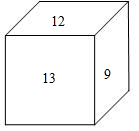 如圖,一個正方體,6個面上分別寫著6個連續的整數,且每個相對面上的兩個數之和相等,如圖所示,你能看到的數為9、12、13,則六個整數之和為69.
如圖,一個正方體,6個面上分別寫著6個連續的整數,且每個相對面上的兩個數之和相等,如圖所示,你能看到的數為9、12、13,則六個整數之和為69.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| x | 1 | 1.1 | 1.2 | 1.3 |
| x2+12x-15 | -2 | -0.59 | 0.84 | 2.29 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com