Question

3．如圖，直線y=x與雙曲線y=$\frac{k}{x}$（k＞0，x＞0）交于點(diǎn)P，PA⊥x軸于點(diǎn)A，S_△PAO=$\frac{9}{2}$

（1）k=9點(diǎn)P的坐標(biāo)為（3，3）；
（2）如圖1，點(diǎn)E的坐標(biāo)為（0，-1），連接PE，過點(diǎn)P作PF⊥PE，交x軸于點(diǎn)F，求點(diǎn)F的坐標(biāo)；
（3）如圖2，將點(diǎn)A向右平移5個單位長度得點(diǎn)M，Q為雙曲線y=$\frac{k}{x}$（x＞0）上一點(diǎn)且滿足S_△QPO=S_△MPO，求點(diǎn)Q的坐標(biāo)；
（4）將△PAO繞點(diǎn)P逆時針旋轉(zhuǎn)一個角α（0°＜α＜180°），記旋轉(zhuǎn)中的△PAO為△PA′O′設(shè)直線PO′、直線A′O′與x軸分別交于點(diǎn)G、H，是否存在這樣的旋轉(zhuǎn)角α，使得△GHO′為等腰三角形？若存在，直接寫出α；若不存在，請說明理由．

Answer 1

分析 （1）由P為y=x與反比例函數(shù)的交點(diǎn)，得到P在y=x上，故設(shè)P（a，a），且a大于0，可得出AP=OA=a，由三角形AOP為直角三角形，且面積已知，利用三角形的面積公式列出關(guān)于a的方程，求出方程的解得到a的值，即可確定出P的坐標(biāo)，將P的坐標(biāo)代入反比例函數(shù)解析式中，即可求出k的值；
（2）根據(jù)題意過P作PF垂直于PE，交x軸于點(diǎn)F，過P作PB垂直于y軸于點(diǎn)B，先由一對對頂角相等及一對直角相等，利用三角形的內(nèi)角和定理得出∠BEP=∠AFP，再由一對直角相等，以及BP=OA=AP，利用AAS可得出三角形BEP與三角形AFP全等，利用全等三角形的對應(yīng)邊相等可得出BE=AF，由OF=OA+AF，即可得出點(diǎn)F的坐標(biāo)；
（3）連接OQ，PQ，過Q作QC⊥x軸于C點(diǎn)，由A的坐標(biāo)及平移的規(guī)律找出M的坐標(biāo)，在x軸上作出M點(diǎn)，連接PM，△POM以O(shè)M為底邊，AP為高，求出△POM的面積，可得出△QPO的面積，由Q在反比例函數(shù)圖象上，設(shè)出Q的坐標(biāo)為Q（m，$\frac{9}{m}$）（m＞0），得出QC與OC，而△QOP的面積=△AOP的面積+直角梯形APQC的面積-△OQC的面積，而△AOP的面積與△QOC的面積相等，故△QOP的面積=直角梯形APQC的面積，由梯形的面積得出關(guān)于m的方程，求出方程的解得到m的值，即可得出Q的坐標(biāo)；
（4）分三種情況分析討論：①當(dāng)GH=O′G時；②當(dāng)GH=HO′時；③當(dāng)GO′=HO′時；分別求得即可．

解答 解：（1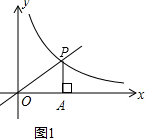）由點(diǎn)P為y=x與反比例函數(shù)y=$\frac{k}{x}$的交點(diǎn)，設(shè)P（a，a）（a＞0），如圖1所示：
可得出PA=OA=a，又S_△PAO=$\frac{9}{2}$，
則$\frac{1}{2}$OA•PA=$\frac{1}{2}$a²=$\frac{9}{2}$，
解得：a=3或a=-3（舍去），
則P（3，3），
將x=3，y=3代入反比例函數(shù)解析式得：3=$\frac{k}{3}$，
則k=3×3=9；
故答案為：9，（3，3）；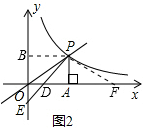
（2）過P作PF⊥PE，交x軸于點(diǎn)F，過P作PB⊥y軸于點(diǎn)B，如圖2所示：
∴BP=AP=3，
∵∠ODE=∠PDF，∠EOD=∠EPF=90°，
∴∠BEP=∠AFP，
在△BEP和△AFP中，
$\left\{\begin{array}{l}{∠EBP=∠FAP=90°}\\{∠BEP=∠AFP}\\{BP=AP}\end{array}\right.$，
∴△BEP≌△AFP（AAS），
∴BE=AF，
∵OA=PA=OB=3，點(diǎn)E的坐標(biāo)為（0，-1），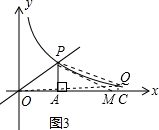
∴BE=4，
∴OF=OA+AF=3+4=7，
∴點(diǎn)F的坐標(biāo)為（7，0）；
（3）連接OQ，PQ，過Q作QC⊥x軸于C點(diǎn)，連接PM，如圖3所示：
∵將A點(diǎn)沿x軸向右平移5個單位為M，
∴M（8，0），
∴OM=8，
∵PA=3，
∴S_△MPO=$\frac{1}{2}$OM•PA=$\frac{1}{2}$×8×3=12，
∵S_△QPO=S_△MPO，
∴S_△QPO=12，
設(shè)Q（m，$\frac{9}{m}$）（m＞0），則有OC=m，QC=$\frac{9}{m}$，
∵PA=OA=3，
∴AC=|m-3|，
∴S_△QPO=S_△PAO+S_梯形APQC-S_△QCO=$\frac{9}{2}$+$\frac{1}{2}$（$\frac{9}{m}$+3）|m-3|-$\frac{9}{2}$=12，
整理得：（m-9）（m+1）=0或者（m+9）（m-1）=0，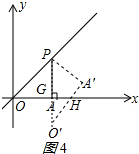
解得：m=9或m=-1（舍去），或者m=1或m=-9（舍去），
∴Q（9，1）或（1，9）；
（4）分三種情況：
當(dāng)GH=O′G時，如圖4所示，
∵∠PO′A′=45°，
∴∠PO′A′=∠GHO′=45°，
∴∠O′GH=90°，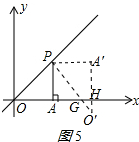
∴PO′⊥x軸
∴α=45°；
當(dāng)GH=HO′時，如圖5，∵∠PO′A′=45°，
∴∠PO′A′=∠HGO′=45°，
∴∠GHO′=90°，
∴A′O′⊥x軸，
∴α=90°；
當(dāng)GO′=HO′時，如圖6，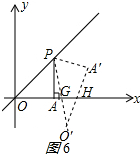
∵∠PO′A′=45°
∴∠GHO′=∠HGO′=67.5°，
∴∠PGA=67.5°，
∵∠PAG=90°，
∴∠APG=22.5°，
∵∠OPA=45°，
∴α=67.5°，
∴當(dāng)α為45°或67.5°或90°時，使△GHO′為等腰三角形．

點(diǎn)評 本題是一次函數(shù)的綜合題，考查了一次函數(shù)圖象上點(diǎn)的坐標(biāo)特征，三角形的面積以及旋轉(zhuǎn)的性質(zhì)，等腰三角形的性質(zhì)，直角三角形的性質(zhì)等知識；本題綜合性強(qiáng)，難度較大，分類討論思想的運(yùn)用是解題的關(guān)鍵．