
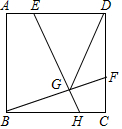
 如圖,正方形ABCD中,點E在邊AD上,點F在邊CD上,AE=CF,EH⊥BF于點G,連接DG.
如圖,正方形ABCD中,點E在邊AD上,點F在邊CD上,AE=CF,EH⊥BF于點G,連接DG.分析 (1)設正方形的邊長為3a.則BC=AD=3a,由tan∠FBC=$\frac{1}{3}$=$\frac{FC}{BC}$,推出AE=FC=a,DE=AD-AE=2a,由DE=6,可得2a=6,求得a=3,在Rt△BFC中,根據BF=$\sqrt{C{F}^{2}+B{C}^{2}}$計算即可.
(2)作DM⊥DG交BF的延長線于M,只要證明△EDG≌△FDM,推出DG=DM,EG=FM,推出△DGM是等腰直角三角形,推出GM=$\sqrt{2}$DG,即可證明.
解答 (1)解:設正方形的邊長為3a.則BC=AD=3a,
∵tan∠FBC=$\frac{1}{3}$=$\frac{FC}{BC}$,
∴AE=FC=a,DE=AD-AE=2a,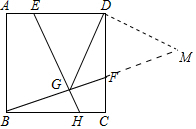
∵DE=6,
∴2a=6,
∴a=3,
在Rt△BFC中,BF=$\sqrt{C{F}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$.
(2)證明:作DM⊥DG交BF的延長線于M.
∵∠GDM=∠ADC=90°,
∴∠EDG=∠FDM,
∵∠DEG+∠DFG=180°,∠DFG+∠DFM=180°,
∴∠DEG=∠DFM,
∵AD=DC,AE=CF,
∴DE=DF,
在△DEG和△DFM中,
$\left\{\begin{array}{l}{∠DEG=∠DFM}\\{DE=DF}\\{∠EDG=∠MDF}\end{array}\right.$,
∴△EDG≌△FDM,
∴DG=DM,EG=FM,
∴△DGM是等腰直角三角形,
∴GM=$\sqrt{2}$DG,
∵GM=FG+FM=FG+EG,
∴EG+FG=$\sqrt{2}$DG.
點評 南通考查正方形的性質、全等三角形的判定和性質、勾股定理、等腰直角三角形的性質和判定等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形解決問題,屬于中考常考題型.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:填空題
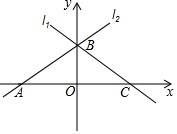 如圖,直線l1與直線l2關于y軸對稱,已知直線l1的函數表達式為y=-$\frac{4}{3}$x+b,點B 坐標為(0,3),則點A坐標為(-$\frac{9}{4}$,0).
如圖,直線l1與直線l2關于y軸對稱,已知直線l1的函數表達式為y=-$\frac{4}{3}$x+b,點B 坐標為(0,3),則點A坐標為(-$\frac{9}{4}$,0).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
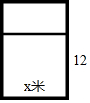 有12米長的木條,要做成一個如圖的窗框,如果假設窗框橫檔的長度為x米,那么窗框的面積是(木條的寬度忽略不計)( )
有12米長的木條,要做成一個如圖的窗框,如果假設窗框橫檔的長度為x米,那么窗框的面積是(木條的寬度忽略不計)( )| A. | x(6-$\frac{3}{2}$x)米2 | B. | x(12-x)米2 | C. | x(6-3x)米2 | D. | x(6-x)米2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
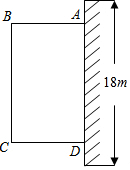 為了改善小區環境,某小區決定要在一塊一邊靠墻(墻長18m)的空地上修建一個矩形綠化帶ABCD,綠化帶一邊靠墻,另三邊用總長為40m的柵欄圍住(如圖),設綠化帶BC邊長為xm,綠化帶的面積為ym2.
為了改善小區環境,某小區決定要在一塊一邊靠墻(墻長18m)的空地上修建一個矩形綠化帶ABCD,綠化帶一邊靠墻,另三邊用總長為40m的柵欄圍住(如圖),設綠化帶BC邊長為xm,綠化帶的面積為ym2.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
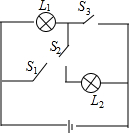 如圖所示電路,任意閉合兩個開關,能使燈L2亮起來的概率是( )
如圖所示電路,任意閉合兩個開關,能使燈L2亮起來的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
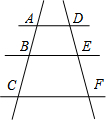 如圖,AD∥BE∥CF,點B,E分別在AC,DF上,DE=2,EF=AB=3,則BC長為( )
如圖,AD∥BE∥CF,點B,E分別在AC,DF上,DE=2,EF=AB=3,則BC長為( )| A. | $\frac{9}{2}$ | B. | 2 | C. | $\frac{7}{2}$ | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com