
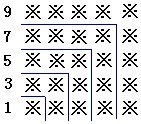
 探索規律:觀察下面由※組成的圖案和算式,解答問題:
探索規律:觀察下面由※組成的圖案和算式,解答問題:分析 (1)根據已知得出連續奇數的和等于數字個數的平方;
(2)根據已知得出連續奇數的和等于數字個數的平方,得出答案即可;
(3)利用以上已知條件得出51+53+55+…+2011+2013=(1+3+5+…+2007+2013)-(1+3+5+…+49),求出即可.
解答 解:(1)由已知得出:
1+3=4=22
1+3+5=9=32
1+3+5+7=19=42
1+3+5+7+9=25=52
依此類推:第n個所代表的算式為:1+3+5+…+(2n-1)=n2;
(1)當2n-1=19,即n=10時,1+3+5+…+19=102.
(2)($\frac{2n+3+1}{2}$)2=(n+2)2;
(3)51+53+55+…+2011+2013
03+105+107+…+2007+2009,
=(1+3+5+…+2011+2013)-(1+3+5+…+49)
=($\frac{2013+1}{2}$)2-($\frac{49+1}{2}$)2=10052-512
=10072-252
=1003104.
故答案為:100,(n+2)2.
點評 此題主要考查了數字變化規律,培養學生通過特例分析從而歸納總結出一般結論的能力.通過分析找到各部分的變化規律后用一個統一的式子表示出變化規律是此類題目的難點.


科目:初中數學 來源: 題型:解答題
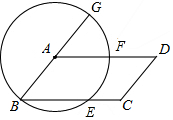 如圖,以□ABCD的頂點A為圓心,AB為半徑作⊙A,分別交BC,AD于E,F兩點,交BA的延長線于G,判斷$\widehat{EF}$和$\widehat{FG}$是否相等,并說明理由.
如圖,以□ABCD的頂點A為圓心,AB為半徑作⊙A,分別交BC,AD于E,F兩點,交BA的延長線于G,判斷$\widehat{EF}$和$\widehat{FG}$是否相等,并說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 88 | B. | 91 | C. | 152 | D. | 155 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com