
| 實驗的稻種數n∕粒 | 800 | 800 | 800 | 800 | 800 |
| 發芽的稻種數m∕粒 | 763 | 757 | 761 | 760 | 758 |
| 發芽的頻率$\frac{m}{n}$ | 0.954 | 0.946 | 0.951 | 0.950 | 0.948 |
分析 利用頻率估計概率得到隨實驗次數的增多,發芽的頻率越來越穩定在0.95左右,由此可估計發芽的機會大約是0.95.
解答 解:根據表中的發芽的頻率,當實驗次數的增多時,發芽的頻率越來越穩定在0.95左右,所以可估計這種大稻發芽的機會大約是0.95,
該農場播種了此稻種2萬粒,那么能發芽的大約有0.95×2=1.9(萬粒).
故答案為0.95;1.9.
點評 本題考查了利用頻率估計概率:大量重復實驗時,事件發生的頻率在某個固定位置左右擺動,并且擺動的幅度越來越小,根據這個頻率穩定性定理,可以用頻率的集中趨勢來估計概率,這個固定的近似值就是這個事件的概率;用頻率估計概率得到的是近似值,隨實驗次數的增多,值越來越精確.


科目:初中數學 來源: 題型:解答題
 如圖,已知四邊形ABCD為⊙O的內接四邊形,AE是⊙O的直徑,連接BE、BD,P為⊙O外一點,連接PA,若∠AEB=40°,AE=12.
如圖,已知四邊形ABCD為⊙O的內接四邊形,AE是⊙O的直徑,連接BE、BD,P為⊙O外一點,連接PA,若∠AEB=40°,AE=12.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
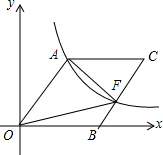 如圖,O為坐標原點,四邊形OACB是菱形,OB在x軸的正半軸上,sin∠AOB=$\frac{4}{5}$,反比例函數y=$\frac{48}{x}$在第一象限內的圖象經過點A,與BC交于點F,則△AOF的面積等于40.
如圖,O為坐標原點,四邊形OACB是菱形,OB在x軸的正半軸上,sin∠AOB=$\frac{4}{5}$,反比例函數y=$\frac{48}{x}$在第一象限內的圖象經過點A,與BC交于點F,則△AOF的面積等于40.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
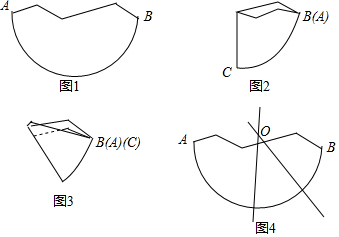 數學課上,老師介紹了利用尺規確定殘缺紙片圓心的方法.小華對數學老師說:“我可以用拆疊紙片的方法確定圓心”.小華的作法如下:
數學課上,老師介紹了利用尺規確定殘缺紙片圓心的方法.小華對數學老師說:“我可以用拆疊紙片的方法確定圓心”.小華的作法如下:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com