
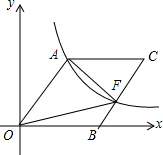
 如圖,O為坐標原點,四邊形OACB是菱形,OB在x軸的正半軸上,sin∠AOB=$\frac{4}{5}$,反比例函數(shù)y=$\frac{48}{x}$在第一象限內(nèi)的圖象經(jīng)過點A,與BC交于點F,則△AOF的面積等于40.
如圖,O為坐標原點,四邊形OACB是菱形,OB在x軸的正半軸上,sin∠AOB=$\frac{4}{5}$,反比例函數(shù)y=$\frac{48}{x}$在第一象限內(nèi)的圖象經(jīng)過點A,與BC交于點F,則△AOF的面積等于40. 分析 過點A作AM⊥x軸于點M,設(shè)OA=a,通過解直角三角形找出點A的坐標,結(jié)合反比例函數(shù)圖象上點的坐標特征即可求出a的值,再根據(jù)四邊形OACB是菱形、點F在邊BC上,即可得出S△AOF=$\frac{1}{2}$S菱形OBCA,結(jié)合菱形的面積公式即可得出結(jié)論.
解答 解:過點A作AM⊥x軸于點M,如圖所示.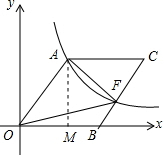
設(shè)OA=a,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=$\frac{4}{5}$,
∴AM=OA•sin∠AOB=$\frac{4}{5}$a,OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=$\frac{3}{5}$a,
∴點A的坐標為($\frac{3}{5}$a,$\frac{4}{5}$a).
∵點A在反比例函數(shù)y=$\frac{48}{x}$的圖象上,
∴$\frac{3}{5}$a×$\frac{4}{5}$a=$\frac{12}{25}$a2=48,
解得:a=10,或a=-10(舍去).
∴AM=8,OM=6,OB=OA=10.
∵四邊形OACB是菱形,點F在邊BC上,
∴S△AOF=$\frac{1}{2}$S菱形OBCA=$\frac{1}{2}$OB•AM=40.
故答案是:40.
點評 本題考查了菱形的性質(zhì)、解直角三角形以及反比例函數(shù)圖象上點的坐標特征,解題的關(guān)鍵是找出S△AOF=$\frac{1}{2}$S菱形OBCA.


 培優(yōu)三好生系列答案
培優(yōu)三好生系列答案 優(yōu)化作業(yè)上海科技文獻出版社系列答案
優(yōu)化作業(yè)上海科技文獻出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
| 實驗的稻種數(shù)n∕粒 | 800 | 800 | 800 | 800 | 800 |
| 發(fā)芽的稻種數(shù)m∕粒 | 763 | 757 | 761 | 760 | 758 |
| 發(fā)芽的頻率$\frac{m}{n}$ | 0.954 | 0.946 | 0.951 | 0.950 | 0.948 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\sqrt{10}$是無理數(shù) | B. | $3<\sqrt{10}<4$ | ||
| C. | 10的平方根是$\sqrt{10}$ | D. | $\sqrt{10}$是10的算術(shù)平方根 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
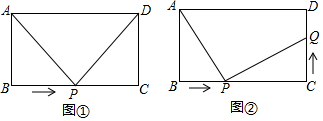
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com