
���� ��1����������̵Ľ�Ͳ���ʽ�M�Ľ⼯�����Д༴�ɣ�
��2�����������ʽ�M�Ľ⼯���������ʽ�M������(sh��)�⣬�ٌ������̼��ɣ�
��3����������̵Ľ�Ͳ���ʽ�M�Ľ⼯�����ɵó��𰸣�
��� �⣺��1���ⷽ��3x-1=0�ã�x=$\frac{1}{3}$��
�ⷽ��$\frac{2}{3}$x+1=0�ã�x=-$\frac{3}{2}$��
�ⷽ��x-��3x+1��=-5�ã�x=2��
�ⲻ��ʽ�M$\left\{\begin{array}{l}{-x+2��x-5}\\{3x-1��-x+2}\end{array}\right.$�ã�$\frac{3}{4}$��x��$\frac{7}{2}$��
���Բ���ʽ�M$\left\{\begin{array}{l}{-x+2��x-5}\\{3x-1��-x+2}\end{array}\right.$���P(gu��n)(li��n)�����Ǣۣ�
�ʴ𰸞飺�ۣ�
��2���ⲻ��ʽ�M$\left\{\begin{array}{l}{x-\frac{1}{2}��1}\\{1+x��-3x+2}\end{array}\right.$�ã�$\frac{1}{4}$��x��$\frac{3}{2}$��
�@��(g��)�P(gu��n)(li��n)���̿�����x-1=0��
�ʴ𰸞飺x-1=0��
��3���ⷽ��3-x=2x�ã�x=1��
�ⷽ��3+x=2��x+$\frac{1}{2}$���ã�x=2��
�ⲻ��ʽ�M$\left\{\begin{array}{l}{x��2x-m}\\{x-2��m}\end{array}\right.$�ã�m��x��2+m��
�߷���3-x=2x��3+x=2��x+$\frac{1}{2}$�������P(gu��n)��x�IJ���ʽ�M$\left\{\begin{array}{l}{x��2x-m}\\{x-2��m}\end{array}\right.$���P(gu��n)(li��n)���̣�
��0��m��1��
��m��ȡֵ������0��m��1��
�c(di��n)�u(p��ng) ���}�����˽�һԪһ�η��̣�һԪһ�η��̵Ľ⣬��һԪһ�β���ʽ�M��֪�R(sh��)�c(di��n)���������P(gu��n)(li��n)���̵Ķ��x�ǽ���}���P(gu��n)�I��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
| ��̖(h��o) | �� | �� | �� | �� | �� | �� | �� | �� |
| �l��(sh��) | 4 | 8 | 12 |  | 24 | 18 | 7 | 3 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ��x���}
| A�� | һ�M��(du��)߅ƽ�У���һ�M��(du��)߅��� | B�� | һ�M��(du��)߅ƽ�У�һ�M��(du��)����� | ||
| C�� | һ�M��(du��)߅ƽ�У�һ�M��(du��)�ǻ��a(b��) | D�� | һ�M��(du��)߅ƽ �У��ɗl��(du��)�Ǿ���� |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ��x���}

| A�� | $\frac{9\sqrt{3}}{4}$ | B�� | 9$\sqrt{3}$ | C�� | $\frac{9\sqrt{2}}{4}$ | D�� | 9$\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
 ��D��AB�ǡ�O��ֱ�����c(di��n)C�ڡ�O�ϣ�OD��AC����BC��D����BD=1���tBC���L(zh��ng)��2��
��D��AB�ǡ�O��ֱ�����c(di��n)C�ڡ�O�ϣ�OD��AC����BC��D����BD=1���tBC���L(zh��ng)��2���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
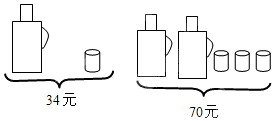
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ��x���}
| A�� | 2��(g��) | B�� | 3��(g��) | C�� | 4��(g��) | D�� | 5��(g��) |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com