
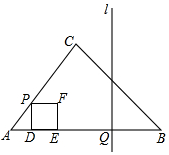
 如圖,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,動點P、Q同時出發,點P沿A-C-B運動,在邊AC的速度為每秒1個單位長度,在邊CB的速度為每秒$\sqrt{2}$個單位長度;點Q沿B-A-B以每秒2個單位長度的速度運動,其中一個動點到達終點時,另一個動點也停止運動,在運動過程中,過點P作AB的垂線與AB交于點D,以PD為邊向由作正方形PDEF;過點Q作AB的垂線l.設正方形PDEF與△ABC重疊部分圖形的面積為y(平方單位),運動時間為t(s).
如圖,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,動點P、Q同時出發,點P沿A-C-B運動,在邊AC的速度為每秒1個單位長度,在邊CB的速度為每秒$\sqrt{2}$個單位長度;點Q沿B-A-B以每秒2個單位長度的速度運動,其中一個動點到達終點時,另一個動點也停止運動,在運動過程中,過點P作AB的垂線與AB交于點D,以PD為邊向由作正方形PDEF;過點Q作AB的垂線l.設正方形PDEF與△ABC重疊部分圖形的面積為y(平方單位),運動時間為t(s).分析 (1)過點P作PD垂直AB,垂足為D,由題意可知,△PDB為等腰直角三角形,從而可求得PD的長;
(2)先求得AD的長,然后依據勾股定理可求得AC的長,由銳角三角函數的定義AD=$\frac{3}{5}$t,當點Q由A到B時.AQ=2(t-3.5),然后由AQ=AD列方程求解即可;如圖2所示:當點Q由B到A時,AP=t,則AD=$\frac{3}{5}$t,BQ=2t,由AD+BQ=7列方程求解即可;
(3)如圖4所示:可分為正方形全部在△ABC的內部、正方形的一部分在△ABC內部、正方形的一半在△ABC的內部三種情況進行計算;
(4)分兩種情形①如圖7中,當△BQH的面積=$\frac{9}{25}$•S△ABC時.②如圖8中,當△AQH的面積=$\frac{9}{25}$•S△ABC時,分別計算即可.
解答 解:(1)如圖1所示: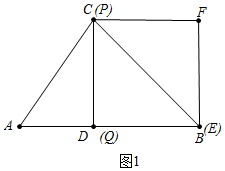
∵PD⊥AB,
∴∠PDB=90°.
又∵∠DBP=45°.
∴PD=BD=BC×$\frac{\sqrt{2}}{2}$=4 $\sqrt{2}$×$\frac{\sqrt{2}}{2}$=4.
故答案為:4.
(2)如圖1所示:∵AB=7,BD=4,
∴AD=3.
∴AC=5.
∴sin∠A=$\frac{4}{5}$,cos∠A=$\frac{3}{5}$.
如圖2所示:當點P在AC上時,AP=t,則PD=$\frac{4}{5}$t,AD=$\frac{3}{5}$t,BQ=2t.
∵AD+BQ=7,
∴$\frac{3}{5}$t+2t=7.
解得:t=$\frac{35}{13}$.
如圖3所示:當點Q由A到B時.AD=$\frac{3}{5}$t,AQ=2(t-3.5).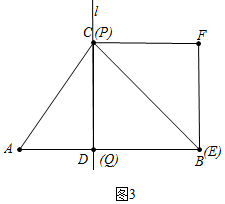
根據題意得:$\frac{3}{5}$t=2(t-3.5).
解得t=5.
綜上所述,當t=$\frac{35}{13}$或t=5時,點D在直線l上.
(3)如圖4所示: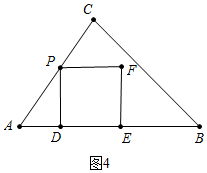
∵PD=$\frac{4}{5}$t,
∴y=DP2=( $\frac{4}{5}$t)2=$\frac{16}{25}$t2.
當點F恰好在BC上時.EF=BB=$\frac{4}{5}$t.
∵AD+DE+EB=7,
∴$\frac{3}{5}$t+$\frac{4}{5}$t+$\frac{4}{5}$t=7.
解得:t=$\frac{35}{11}$.
∴當0<t≤$\frac{35}{11}$時,S=$\frac{16}{25}$t2.
當 $\frac{35}{11}$<t≤5時,如圖5所示.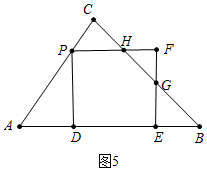
∵AQ=$\frac{3}{5}$t,DE=PD=$\frac{4}{5}$t,
∴EB=7-$\frac{7}{5}$t.
∵∠GEB=90°,∠B=45°,
∴EG=EB=7-$\frac{7}{5}$t.
∴FG=FE-GE=$\frac{11}{5}$t-7.
∴y=PD2-$\frac{1}{2}$FH•FG=-$\frac{89}{50}$t2+$\frac{77}{5}$t-$\frac{49}{2}$.
當5<t≤7時,如圖6所示.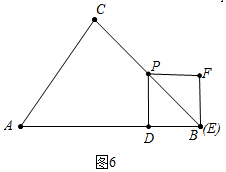
∵AD=AC×$\frac{3}{5}$+$\frac{\sqrt{2}}{2}$CP=3+(t-5)=t-2,
∴DB=7-(t-2)=9-t.
∴y=$\frac{1}{2}$(9-t)2=$\frac{1}{2}$t2-9t+$\frac{81}{2}$.
綜上所述,y與t的關系式為S=$\left\{\begin{array}{l}{\frac{16}{25}{t}^{2}}&{(0<t≤\frac{35}{11})}\\{-\frac{89}{50}{t}^{2}+\frac{77}{5}t-\frac{49}{2}}&{(\frac{35}{11}<t≤5)}\\{\frac{1}{2}{t}^{2}-9t+\frac{81}{2}}&{(5<t≤7)}\end{array}\right.$.
(4)①如圖7中,當△BQH的面積=$\frac{9}{25}$•S△ABC時,$\frac{1}{2}$BQ2=$\frac{9}{25}$×14,BQ=$\frac{6\sqrt{7}}{5}$,∴t=$\frac{3\sqrt{7}}{5}$或7-$\frac{3\sqrt{7}}{5}$時,直線1將△ABC的面積分為9:16兩部分.
②如圖8中,當△AQH的面積=$\frac{9}{25}$•S△ABC時,$\frac{1}{2}$•AQ•$\frac{4}{3}$AQ=$\frac{9}{25}$×14,AQ=$\frac{3}{5}$$\sqrt{21}$,∴t=$\frac{3}{10}$$\sqrt{21}$或7-$\frac{3}{10}$$\sqrt{21}$時,直線1將△ABC的面積分為9:16兩部分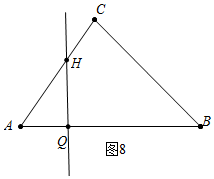
綜上所述,t=$\frac{3\sqrt{7}}{5}$s或(7-$\frac{3\sqrt{7}}{5}$)s或$\frac{3}{10}$$\sqrt{21}$s或(7-$\frac{3}{10}$$\sqrt{21}$)s時,直線1將△ABC的面積分為9:16兩部分.
點評 本題主要考查的是四邊形的綜合應用,解答本題主要應用了正方形的性質、等腰直角三角形的性質,特殊銳角三角函數值,銳角三角函數的定義,根據題意畫出圖形,并用含t的式子表示相關線段的長度是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
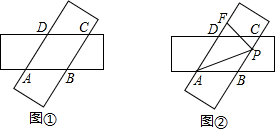
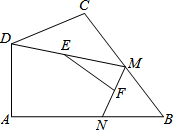 如圖,在四邊形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,點M、N分別為線段BC、AB上的動點,點E、F分別為DM、MN的中點,則EF長度的最大值為( )
如圖,在四邊形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,點M、N分別為線段BC、AB上的動點,點E、F分別為DM、MN的中點,則EF長度的最大值為( )| A. | 2 | B. | 3 | C. | 4 | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
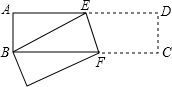 如圖,已知,矩形ABCD中,AB=3cm,AD=9cm,將此矩形折疊,使點B與點D重合,折痕為EF,則AE的長為( )
如圖,已知,矩形ABCD中,AB=3cm,AD=9cm,將此矩形折疊,使點B與點D重合,折痕為EF,則AE的長為( )| A. | 3 | B. | 4 | C. | 5 | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com