

分析 (1)由旋轉的性質可知:AF=AG,∠DAF=∠BAG,接下來在證明∠GAE=∠FAE,然后依據SAS證明△GAE≌△FAE即可;
(2)將△ABM逆時針旋轉90°得△ADM′.在△NM′D中依據勾股定理可證明NM′2=ND2+DM′2,接下來證明△AMN≌△ANM′,于的得到MN=NM′,最后再由BM=DM′證明即可.
解答 解:(1)由旋轉的性質可知:AF=AG,∠DAF=∠BAG.
∵四邊形ABCD為正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中$\left\{\begin{array}{l}{AG=AF}\\{∠GAE=∠FAE}\\{AE=AE}\end{array}\right.$,
∴△GAE≌△FAE(SAS);
(2)如圖所示:將△ABM逆時針旋轉90°得△ADM′.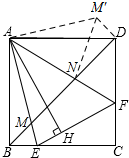
∵四邊形ABCD為正方形,
∴∠ABD=∠ADB=45°.
由旋轉的性質可知:∠ABM=∠ADM′=45°,BE=DM′.
∴∠NDM′=90°.
∴NM′2=ND2+DM′2.
∵∠EAM′=90°,∠EAF=45°,
∴∠EAF=∠FAM′=45°.
在△AMN和△ANM′中,$\left\{\begin{array}{l}{AM=AM′}\\{∠MAN=M′AN}\\{AN=AN}\end{array}\right.$,
∴△AMN≌△ANM′(SAS).
∴MN=NM′.
又∵BM=DM′,
∴MN2=ND2+BM2.
點評 本題主要考查的是四邊形的綜合應用,解答本題主要應用了旋轉的性質、全等三角形的性質和判定、勾股定理的應用,正方形的性質,依據旋轉的性質構造全等三角形和直角三角形是解題的關鍵.


科目:初中數學 來源: 題型:解答題
 如圖,用(0,0)表示A點的位置,用(3,1)表示B點的位置,那么:
如圖,用(0,0)表示A點的位置,用(3,1)表示B點的位置,那么:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
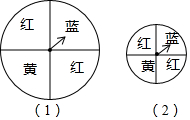 如圖,兩個用來搖獎的轉盤,其中說法正確的是( )
如圖,兩個用來搖獎的轉盤,其中說法正確的是( )| A. | 轉盤(1)中藍色區域的面積比轉盤(2)中的藍色區域面積要大,所以搖轉盤(1)比搖轉盤(2)時,藍色區域得獎的可能性大 | |
| B. | 兩個轉盤中指針指向藍色區域的機會一樣大 | |
| C. | 轉盤(1)中,指針指向紅色區域的概率是$\frac{1}{3}$ | |
| D. | 在轉盤(2)中只有紅、黃、藍三種顏色,指針指向每種顏色的概率都是$\frac{1}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
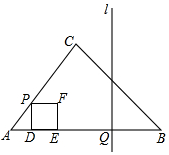 如圖,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,動點P、Q同時出發,點P沿A-C-B運動,在邊AC的速度為每秒1個單位長度,在邊CB的速度為每秒$\sqrt{2}$個單位長度;點Q沿B-A-B以每秒2個單位長度的速度運動,其中一個動點到達終點時,另一個動點也停止運動,在運動過程中,過點P作AB的垂線與AB交于點D,以PD為邊向由作正方形PDEF;過點Q作AB的垂線l.設正方形PDEF與△ABC重疊部分圖形的面積為y(平方單位),運動時間為t(s).
如圖,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,動點P、Q同時出發,點P沿A-C-B運動,在邊AC的速度為每秒1個單位長度,在邊CB的速度為每秒$\sqrt{2}$個單位長度;點Q沿B-A-B以每秒2個單位長度的速度運動,其中一個動點到達終點時,另一個動點也停止運動,在運動過程中,過點P作AB的垂線與AB交于點D,以PD為邊向由作正方形PDEF;過點Q作AB的垂線l.設正方形PDEF與△ABC重疊部分圖形的面積為y(平方單位),運動時間為t(s).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 小明的手機沒電了,現有一個只含A,B,C,D四個同型號插座的插線板(如圖,假設每個插座都適合所有的充電插頭,且被選中的可能性相同),請計算:
小明的手機沒電了,現有一個只含A,B,C,D四個同型號插座的插線板(如圖,假設每個插座都適合所有的充電插頭,且被選中的可能性相同),請計算:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com