
分析 (1)根據(jù)一元二次方程的根的判別式,直接計算即可;
(2)根據(jù)求根公式,求出兩根,由拋物線與x軸的兩個交點的橫坐標(biāo)都為正整數(shù),求出m的值,可得拋物線解析式.
解答 解:(1)由題意可知,△=b2-4ac=(3m+1)2-4m×3=(3m-1)2>0,
解得:m≠$\frac{1}{3}$,
∵二次函數(shù)的圖象與x軸有兩個交點,
∴m≠0,
∴當(dāng)m≠$\frac{1}{3}$且m≠0時,此二次函數(shù)的圖象與x軸有兩個交點;
(2)有求根公式,得:x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-(3m+1)±\sqrt{(3m+1)^{2}-12m}}{2m}$,
∴x1=-3,x2=-$\frac{1}{m}$,
∵拋物線與x軸兩個交點的橫坐標(biāo)均為整數(shù),且m為正整數(shù),
∴m=1,
∴拋物線的解析式為:y=x2+4x+3;
點評 本題主要考查了拋物線與x軸的交點,熟知拋物線與x軸的交點坐標(biāo)的橫坐標(biāo)即相應(yīng)的一元二次方程的解是解決此題的關(guān)鍵.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
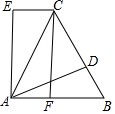 如圖,△ABC是等邊三角形,D是BC上一點,△ABD經(jīng)旋轉(zhuǎn)后到達△ACE的位置.
如圖,△ABC是等邊三角形,D是BC上一點,△ABD經(jīng)旋轉(zhuǎn)后到達△ACE的位置.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 分別畫出滿足下列條件的點:(尺規(guī)作圖,請保留組圖痕跡,不寫作法).
分別畫出滿足下列條件的點:(尺規(guī)作圖,請保留組圖痕跡,不寫作法).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
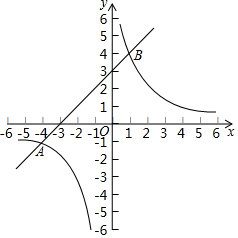 已知:如圖,在平面直角坐標(biāo)系xOy中,反比例函數(shù)y1=$\frac{m}{x}$的圖象與一次函數(shù)y2=kx+b的圖象交于點A(-4,-1)和點B(1,n).
已知:如圖,在平面直角坐標(biāo)系xOy中,反比例函數(shù)y1=$\frac{m}{x}$的圖象與一次函數(shù)y2=kx+b的圖象交于點A(-4,-1)和點B(1,n).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,直線y=ax-4(a≠0)與雙曲線y=$\frac{k}{x}$只有一個公共點A(1,-2).
如圖,直線y=ax-4(a≠0)與雙曲線y=$\frac{k}{x}$只有一個公共點A(1,-2).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com