
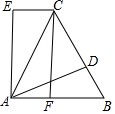
 如圖,△ABC是等邊三角形,D是BC上一點(diǎn),△ABD經(jīng)旋轉(zhuǎn)后到達(dá)△ACE的位置.
如圖,△ABC是等邊三角形,D是BC上一點(diǎn),△ABD經(jīng)旋轉(zhuǎn)后到達(dá)△ACE的位置.分析 (1)根據(jù)△ABD經(jīng)旋轉(zhuǎn)后到達(dá)△ACE的位置,可得旋轉(zhuǎn)中心,再根據(jù)旋轉(zhuǎn)的性質(zhì)以及等邊三角形的性質(zhì),即可得出∠EAD的度數(shù);
(2)根據(jù)一組對邊平行且相等的四邊形是平行四邊形進(jìn)行證明即可.
解答  解:(1)由旋轉(zhuǎn)可得,旋轉(zhuǎn)中心是點(diǎn)A,∠BAD=∠CAE,
解:(1)由旋轉(zhuǎn)可得,旋轉(zhuǎn)中心是點(diǎn)A,∠BAD=∠CAE,
∵△ABC是等邊三角形,
∴∠BAD+∠CAD=∠CAE+∠CAD=60°,
∴∠EAD=60°;
故答案為:A,60;
(2)∵∠CAB=∠B=∠ACE=60°,
∴AF∥CE,
又∵AF=BD=EC,
∴四邊形AFCE是平行四邊形.
點(diǎn)評 本題主要考查了旋轉(zhuǎn)的性質(zhì)以及平行四邊形的判定,解決問題的關(guān)鍵是運(yùn)用旋轉(zhuǎn)前、后的圖形全等進(jìn)行解題.


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | -a+b+c+d=-(a-b)-(-c-d) | B. | x-(y-z)=x-y-z | ||
| C. | x+2y-2z=x-2(z+y) | D. | -(x-y+z)=-x-y-z |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
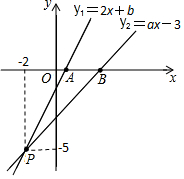 如圖,已知函數(shù)y1=2x+b和y2=ax-3的圖象交于點(diǎn)P (-2,-5),這兩個函數(shù)的圖象與x軸分別交于點(diǎn)A、B.
如圖,已知函數(shù)y1=2x+b和y2=ax-3的圖象交于點(diǎn)P (-2,-5),這兩個函數(shù)的圖象與x軸分別交于點(diǎn)A、B.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,C,D是線段AB上兩點(diǎn),D是線段AC的中點(diǎn),若AB=10cm,BC=4cm,則AD的長等于多少?
如圖,C,D是線段AB上兩點(diǎn),D是線段AC的中點(diǎn),若AB=10cm,BC=4cm,則AD的長等于多少?查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
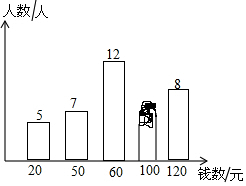 小明調(diào)查了學(xué)校50名同學(xué)本學(xué)期購買課外書的花費(fèi)情況,并將結(jié)果繪制成了下面的統(tǒng)計圖,由于不小心滴上了墨水,導(dǎo)致花費(fèi)為100元的人數(shù)看不清楚了.求出這50名學(xué)生本學(xué)期購買課外書花費(fèi)的眾數(shù)、中位數(shù)和平均數(shù).
小明調(diào)查了學(xué)校50名同學(xué)本學(xué)期購買課外書的花費(fèi)情況,并將結(jié)果繪制成了下面的統(tǒng)計圖,由于不小心滴上了墨水,導(dǎo)致花費(fèi)為100元的人數(shù)看不清楚了.求出這50名學(xué)生本學(xué)期購買課外書花費(fèi)的眾數(shù)、中位數(shù)和平均數(shù).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com