Question

18．在△ABC中，∠A=70°．

（1）如圖①∠ABC，∠ACB 的平分線相交于點O，則∠BOC=55°；
（2）如圖②△ABC的外角∠CBD，∠BCE 的平分線相交于點O'，則∠BO'C=55°；
（3）探究
探究一：如圖③，△ABC的內角∠ABC的平分線與其外角∠ACD 的平分線相交于點O，設∠A=n°，求∠BOC的度數．（用n的代數式表示）
探究二：已知：四邊形ABCD的內角∠ABC的平分線所在直線與其外角∠DCE的平分線所在直線
相交于點O，∠A=n°，∠D=m°
①如圖④，若∠A+∠D≥180°，則∠BOC=$\frac{1}{2}$（n°+m°）-90°（用m、n的代數式表示）
②如圖⑤，若∠A+∠D＜180°，則∠BOC=90°-$\frac{1}{2}$（n°+m°）（用m、n的代數式表示）

Answer 1

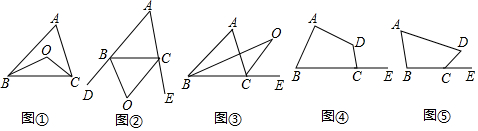
分析 （1）求出∠ABC+∠ACB，根據角平分線定義求出∠OBC+∠OCB，根據三角形內角和定理求出即可；
（2）根據三角形的一個外角等于與它不相鄰的兩個內角的和以及角平分線的定義表示出∠OBC與∠OCB，然后再根據三角形的內角和定理列式整理即可得解；
（3）探究
探究一：根據提供的信息，根據三角形的一個外角等于與它不相鄰的兩個內角的和，用∠A與∠1表示出∠2，再利用∠O與∠1表示出∠2，然后整理即可得到∠BOC的度數．
探究二：①根據四邊形的內角和定理表示出∠BCD，再表示出∠DCE，然后根據角平分線的定義可得∠OBC=$\frac{1}{2}$∠ABC，∠OCE=$\frac{1}{2}$∠DCE，三角形的一個外角等于與它不相鄰的兩個內角的和可得∠BOC+∠OBC=∠OCE，然后整理即可得解；
②同①的思路求解即可．

解答 解：（1）∵∠A=70°，
∴∠ABC+∠ACB=180°-∠A=110°，
∵BO、CO分別是∠ABC和∠ACB的平分線，
∴∠OBC=$\frac{1}{2}$∠ABC，∠OCB=$\frac{1}{2}$∠ACB，
∴∠OBC+∠OCB=$\frac{1}{2}$×110°=55°，
∴在△BOC中，∠BOC=180°-（∠OBC+∠OCB）=125°；

（2）∵∠DBC=∠A+∠ACB，∠ECB=∠A+∠ABC，
∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC=180°+∠A，
∵BO、CO分別是△ABC兩個外角∠CBD和∠BCE的平分線，
∴∠OBC=$\frac{1}{2}$∠DBC，∠OCB=$\frac{1}{2}$∠ECB，
∴∠OBC+∠OCB=$\frac{1}{2}$（180°+∠A），
∴∠BOC=180°-（∠OBC+∠OCB）=180°-$\frac{1}{2}$（180°+∠A）=90°-$\frac{1}{2}$∠A=55°；

（3）探究
探究一：∵BO和CO分別是∠ABC和∠ACD的角平分線，
∴∠OBC=$\frac{1}{2}$∠ABC，∠OCE=$\frac{1}{2}$∠ACD，
又∵∠ACD是△ABC的一外角，
∴∠ACD=∠A+∠ABC，
∴∠OCE=$\frac{1}{2}$（∠A+∠ABC）=$\frac{1}{2}$∠A+∠OBC，
∵∠OCE是△BOC的一外角，
∴∠BOC=∠OCE-∠OBC=$\frac{1}{2}$∠A+∠OBC-∠OBC=$\frac{1}{2}$∠A=$\frac{1}{2}$n°；
探究二：①由四邊形內角和定理得，∠BCD=360°-∠A-∠D-∠ABC，
∴∠DCE=180°-（360°-∠A-∠D-∠ABC）=∠A+∠D+∠ABC-180°，
由三角形的外角性質得，∠DCE=∠A+∠D+∠ABC，∠OCE=∠O+∠OBC，
∵BO、CO分別是∠ABC和∠DCE的平分線，
∴∠OBC=$\frac{1}{2}$∠ABC，∠OCE=$\frac{1}{2}$∠DCE，
∴∠BOC+∠OBC=$\frac{1}{2}$（∠A+∠D+∠ABC-180°）=$\frac{1}{2}$（∠A+∠D）+$\frac{1}{2}$∠ABC-90°，
∴∠BOC=$\frac{1}{2}$（∠A+∠D）-90°，
∵∠A=n°，∠D=m°，
∴∠BOC=$\frac{1}{2}$（n°+m°）-90°；
②同①可求，∠BOC=90°-$\frac{1}{2}$（n°+m°）．
故答案為：55；55；$\frac{1}{2}$（n°+m°）-90°；90°-$\frac{1}{2}$（n°+m°）．

點評 本題考查了多邊形的內角和公式，三角形的外角性質與內角和定理，熟記三角形的一個外角等于與它不相鄰的兩個內角的和是解題的關鍵，讀懂題目提供的信息，然后利用提供信息的思路也很重要．