
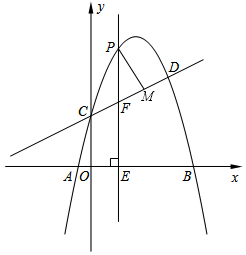
 如圖,拋物線y=-x2+bx+c與直線y=x+4交于C、D兩點(diǎn),其中點(diǎn)C在y軸上,點(diǎn)D的坐標(biāo)為(6,7).點(diǎn)P是y軸右側(cè)的拋物線上一動(dòng)點(diǎn),過點(diǎn)P作PE⊥x軸于點(diǎn)E,交CD于點(diǎn)F,作PM⊥CD于點(diǎn)M.
如圖,拋物線y=-x2+bx+c與直線y=x+4交于C、D兩點(diǎn),其中點(diǎn)C在y軸上,點(diǎn)D的坐標(biāo)為(6,7).點(diǎn)P是y軸右側(cè)的拋物線上一動(dòng)點(diǎn),過點(diǎn)P作PE⊥x軸于點(diǎn)E,交CD于點(diǎn)F,作PM⊥CD于點(diǎn)M.分析 (1)易求C點(diǎn)的坐標(biāo),再把C和D點(diǎn)的坐標(biāo)代入拋物線y=-x2+bx+c可求出b和c的值則拋物線的解析式可求出;若要求sin∠PFM的值可轉(zhuǎn)化為求sin∠OCE;
(2)①設(shè)點(diǎn)P的橫坐標(biāo)為m,則P(m,-m2+$\frac{13}{2}$m+4),F(xiàn)(m,m+4).則PF=yP-yF=(-m2+$\frac{13}{2}$m+4)-( m+4)=-m2+6m,進(jìn)而根據(jù)二次函數(shù)的性質(zhì)即可求出線段PM長的最大值;
②若以O(shè)、C、P、F為頂點(diǎn)的四邊形是平行四邊形,只要PF=OC=4,構(gòu)建方程即可解決問題.
解答 解:(1)C在直線y=x+4上,
∴C(0,4).
∵點(diǎn)C(0,4)、D(6,7)在拋物線y=-x2+bx+c上,
∴$\left\{\begin{array}{l}{c=4}\\{-36+6b+c=7}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{b=\frac{13}{2}}\\{c=4}\end{array}\right.$,
∴拋物線的解析式為:y=-x2+$\frac{13}{2}$x+4.
∵直線CD的解析式為y=x+4,
∴易知∠PFM=45°,
∴sin∠PFM=sin45°=$\frac{\sqrt{2}}{2}$
(2)①設(shè)點(diǎn)P的橫坐標(biāo)為m,則P(m,-m2+$\frac{13}{2}$m+4),F(xiàn)(m,m+4).
∵PF=yP-yF=(-m2+$\frac{13}{2}$m+4)-( m+4)=-m2+$\frac{11}{2}$m,
在Rt△PFM中,PM=PF sin∠PFM=$\frac{\sqrt{2}}{2}$(-m2+$\frac{11}{2}$m)
=-$\frac{\sqrt{2}}{2}$(m-$\frac{11}{4}$)2+$\frac{121\sqrt{2}}{32}$,
∵-$\frac{\sqrt{2}}{2}$<0,
∴當(dāng)m=$\frac{11}{4}$時(shí),PM的最大值為$\frac{121\sqrt{2}}{32}$.
∴PM=$\frac{\sqrt{2}}{2}$(-m2+$\frac{11}{2}$m),PM的最大值為$\frac{121\sqrt{2}}{32}$.
②∵PF∥OC,
若以O(shè)、C、P、F為頂點(diǎn)的四邊形是平行四邊形,只要PF=OC=4,
由題意:(-m2+$\frac{13}{2}$m+4)-( m+4)=4和(m+4)-(-m2+$\frac{13}{2}$m+4)=4,
解得m=$\frac{11±\sqrt{57}}{4}$或$\frac{11+\sqrt{185}}{4}$或$\frac{11-\sqrt{185}}{4}$(舍棄)
∴當(dāng)m為$\frac{11±\sqrt{57}}{4}$或$\frac{11-\sqrt{185}}{4}$時(shí),以O(shè)、C、P、F為頂點(diǎn)的四邊形是平行四邊形.
點(diǎn)評(píng) 本題是二次函數(shù)綜合題型,一次函數(shù)的應(yīng)用、平行四邊形的性質(zhì)、銳角三角函數(shù)、一元二次方程等知識(shí),解題的關(guān)鍵是靈活運(yùn)用所學(xué)知識(shí)解決問題,學(xué)會(huì)構(gòu)建二次函數(shù)解決最值問題,學(xué)會(huì)用方程的思想思考問題,屬于中考?jí)狠S題.


 教學(xué)練新同步練習(xí)系列答案
教學(xué)練新同步練習(xí)系列答案 課前課后同步練習(xí)系列答案
課前課后同步練習(xí)系列答案 課堂小作業(yè)系列答案
課堂小作業(yè)系列答案 黃岡小狀元口算速算練習(xí)冊系列答案
黃岡小狀元口算速算練習(xí)冊系列答案 成功訓(xùn)練計(jì)劃系列答案
成功訓(xùn)練計(jì)劃系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,AB為⊙O的直徑,CD⊥AB于點(diǎn)E,交⊙O于點(diǎn)D,OF⊥AC于點(diǎn)F,且OF=1.
如圖,AB為⊙O的直徑,CD⊥AB于點(diǎn)E,交⊙O于點(diǎn)D,OF⊥AC于點(diǎn)F,且OF=1.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
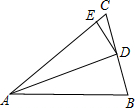 如圖,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.則∠EDC的大小是( )
如圖,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.則∠EDC的大小是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
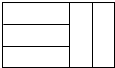 五個(gè)完全相同的小長方形拼成如圖所示的大長方形,大長方形的周長是32cm,則小長方形的面積是( )
五個(gè)完全相同的小長方形拼成如圖所示的大長方形,大長方形的周長是32cm,則小長方形的面積是( )| A. | 8cm2 | B. | 10cm2 | C. | 12cm2 | D. | 16cm2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2x | B. | -2x | C. | 4x | D. | -4x4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
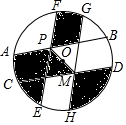 如圖,一個(gè)半徑為2cm的圓盤被分割成十個(gè)區(qū)域.其中,弦AB、CD關(guān)于圓心O對(duì)稱,EF、GH關(guān)于圓心O對(duì)稱,向盤中投擲一物體,則物體落在陰影部分的概率為$\frac{1}{2}$.
如圖,一個(gè)半徑為2cm的圓盤被分割成十個(gè)區(qū)域.其中,弦AB、CD關(guān)于圓心O對(duì)稱,EF、GH關(guān)于圓心O對(duì)稱,向盤中投擲一物體,則物體落在陰影部分的概率為$\frac{1}{2}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 第一個(gè) | B. | 第二個(gè) | C. | 第三個(gè) | D. | 第四個(gè) |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com