Question

11．為迎接河南省第30屆青少年科技創新大賽，某中學向七年級學生征集科幻畫作品，李老師從七年級12個班中隨機抽取了A、B、C、D四個班，對征集到的作品的數量進行了分析統計，制作了兩幅不完整的統計圖（如圖）
（1）李老師所調查的4個班征集到作品共12件，其中B班征集到作品3，請把圖補充完整；
（2）李老師所調查的四個班平均每個班征集到作品多少件？請估計全年級共征集到作品多少件？
（3）如果全年級參展作品中有5件獲得一等獎，其中有3名作者是男生，2名作者是女生．現在要抽兩人去參加學校總結表彰座談會，用樹狀圖或列表法求出恰好抽中一男一女的概率．

Answer 1

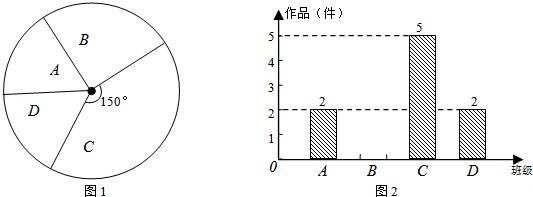
分析 （1）根據C在扇形圖中的角度求出所占的份數，再根據C的人數是5，列式進行計算即可求出作品的件數，然后減去A、C、D的件數即為B的件數；
（2）求出平均每一個班的作品件數，然后乘以班級數14，計算即可得解；
（3）首先根據題意畫出樹狀圖，然后由樹狀圖求得所有等可能的結果與恰好抽中一男一女的情況，再利用概率公式即可求得答案．

解答 解：（1）根據題意得：
調查的4個班征集到作品數為：5÷$\frac{150}{360}$=12（件），
B班作品的件數為：12-2-5-2=3（件），
補圖如下：

故答案為：12；3；
（2）王老師所調查的四個班平均每個班征集作品是：12÷4=3（件），
全校共征集到的作品：3×14=42（件）；
（3）畫樹狀圖得：

∵共有20種等可能的結果，恰好抽中一男一女的有12種情況，
∴恰好抽中一男一女的概率為：$\frac{12}{20}$=$\frac{3}{5}$．

點評 此題考查了列表法或樹狀圖法求概率以及條形統計圖與扇形統計圖．用到的知識點為：概率=所求情況數與總情況數之比．讀懂統計圖，從不同的統計圖中得到必要的信息是解決問題的關鍵．