
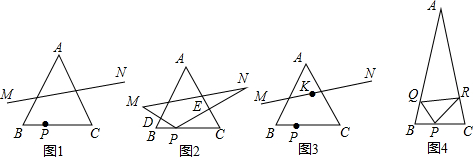
分析 【發(fā)現(xiàn)】當(dāng)點P為BC的中點時,MN最短,求出此時MN的長度,當(dāng)點P與點B(或C)重合時,BN(或CM)最長,求出此時BN的長度;
【探究】(1)解直角三角形即可得到結(jié)論;
(2)如圖2,分別過點M,N作直線BC的垂線MF,NG,垂足分別是F,G,過點M作MH⊥NG垂足為H.解直角三角形得到MF=$\frac{\sqrt{3}}{2}$x,PF=$\frac{3}{2}$x,NG=$\frac{\sqrt{3}}{2}$(4-x),PG=$\frac{3}{2}$(4-x),根據(jù)勾股定理即可得到結(jié)論;
(3)由MN=3$\sqrt{7}$,得到MN2=63,把y=63時代入3(x-2)2+36=63,即可得到結(jié)論;
【拓展】如圖3,分別過點M,N作直線BC的垂線MF,NG,垂足分別是F,G,連接MG,過MN的中點K,作KT⊥BC于點T,交MG于點S.由MF∥KT∥NG,且點K為MN的中點,得到KS是△MNG的中位線,ST是△GMF的中位線,由【探究】中的過程可知,若設(shè)PB=x,則有PC=4-x,MF=$\frac{\sqrt{3}}{2}$x,NG=$\frac{\sqrt{3}}{2}$(4-x),根據(jù)三角形的中位線的性質(zhì)即可得到結(jié)論;
【應(yīng)用】過BC的中點P作AB,AC的對稱點M,N,連接MN交AB與Q,交AC于R,則此時△PQR周長最小,根據(jù)三角形和四邊形的內(nèi)角和得到∠B=∠C=75°,∠MPN=150°,得到MN∥BC,PQ=PB=1,同理PR=PC=1,解直角三角形得到QR=2×$\frac{\sqrt{3}}{2}$PQ=$\sqrt{3}$,于是得到結(jié)論.
解答 解:【發(fā)現(xiàn)】當(dāng)AP的長最小時,AP⊥BC,即點P為BC的中點時,
此時E、F分別為AB、AC的中點,
∴PE=$\frac{1}{2}$AC,PF=$\frac{1}{2}$AB,EF=$\frac{1}{2}$BC,
∴MN=ME+EF+FN=PE+EF+PF=6;
當(dāng)點P和點B重合時,
此時G(H)為AB(AC)的中點,
∴CG=2$\sqrt{3}$BH=2$\sqrt{3}$,
BN=4$\sqrt{3}$;
故答案為:4$\sqrt{3}$,6;
【探究】(1)PM=2PD=2×$\frac{\sqrt{3}}{2}$PB=$\sqrt{3}$x,PN=2PE=2×$\frac{\sqrt{3}}{2}$PC=2×$\frac{\sqrt{3}}{2}$(4-x)=$\sqrt{3}$(4-x);
故答案為:$\sqrt{3}$x,$\sqrt{3}$(4-x);
(2)如圖2,分別過點M,N作直線BC的垂線MF,NG,垂足分別是F,G,過點M作MH⊥NG垂足為H.
∵在Rt△PMF中,∠MPF=30°,PM=$\sqrt{3}$x,
∴MF=$\frac{\sqrt{3}}{2}$x,PF=$\frac{3}{2}$x,
同理,在Rt△PNG中,∠NPG=30°,PN=$\sqrt{3}$(4-x),
∴NG=$\frac{\sqrt{3}}{2}$(4-x),PG=$\frac{3}{2}$(4-x),
∵四邊形MFGH是矩形,則有
NH=NG-HG=NG-MF=$\frac{\sqrt{3}}{2}$(4-x)-$\frac{\sqrt{3}}{2}$x=$\sqrt{3}$(2-x),
MH=FG=PF+PG=$\frac{3}{2}$x+$\frac{3}{2}$(4-x)=6,
∴在Rt△MNH中,由勾股定理得,
MN2=NH2+MH2=3(x-2)2+36,
則y=3(x-2)2+36,
∵0≤x≤4,且當(dāng)x=2時,y最小值=36;當(dāng)x=0或4時,y最大值=48,
∴36≤y≤48;
(3)∵M(jìn)N=3$\sqrt{7}$,MN2=63,
∴當(dāng)y=63時,即3(x-2)2+36=63,
∴x=5或-1,
∴當(dāng)點P在B點右側(cè)距離為5,或者在點P在B點左側(cè)距離為1的位置處,均有線段MN=3$\sqrt{7}$;
【拓展】如圖3,分別過點M,N作直線BC的垂線MF,NG,垂足分別是F,G,連接MG,過MN的中點K,作KT⊥BC于點T,交 MG于點S.
MG于點S.
∵M(jìn)F∥KT∥NG,且點K為MN的中點,
∴KS是△MNG的中位線,
ST是△GMF的中位線,
由【探究】中的過程可知,若設(shè)PB=x,則有PC=4-x,MF=$\frac{\sqrt{3}}{2}$x,NG=$\frac{\sqrt{3}}{2}$(4-x),
由三角形中位線性質(zhì)可得,ST=$\frac{1}{2}$MF=$\frac{\sqrt{3}}{4}$x,KS=$\frac{1}{2}$NG=$\frac{\sqrt{3}}{4}$(4-x),
∴KT=ST+KS=$\frac{\sqrt{3}}{4}$x+$\frac{\sqrt{3}}{4}$(4-x)=$\sqrt{3}$,
因此,在點P運動過程中,MN的中點 K到BC邊距離始終等于定值$\sqrt{3}$,且為
等邊△ABC高的一半,所以MN的中點K經(jīng)過的路線恰為等邊△ABC的中位線,其路線長為2.
【應(yīng)用】過BC的中點P作AB,AC的對稱點M,N,連接MN交AB與Q,交AC于R,
則此時△PQR周長最小,
∵∠BAC=30°,
∴∠B=∠C=75°,∠MPN=150°,
∴∠M=∠N=15°,
∴∠MQB=∠PQB=∠B=75°,
∴MN∥BC,PQ=PB=1,
同理PR=PC=1,
∵AP⊥BC,
∴AP⊥MN.
∵∠PQR=180°-75°-75°=30°,
∴QR=2×$\frac{\sqrt{3}}{2}$PQ=$\sqrt{3}$,
∴△PQR周長的最小值是2+$\sqrt{3}$.
故答案為:2+$\sqrt{3}$.
點評 本題考查了軸對稱的性質(zhì),等邊三角形的性質(zhì),等腰三角形的性質(zhì),三角形的中位線的性質(zhì),解直角三角形,勾股定理,正確的作出輔助線是解題的關(guān)鍵.


科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
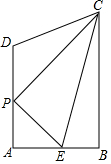 如圖,在梯形ABCD中,AD∥BC,∠A=90°,AB=6,BC=10,AD=7,點P在邊AD上運動(不與點A,D重合),E是邊AB上一點,連結(jié)PC,PE,EC.
如圖,在梯形ABCD中,AD∥BC,∠A=90°,AB=6,BC=10,AD=7,點P在邊AD上運動(不與點A,D重合),E是邊AB上一點,連結(jié)PC,PE,EC.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. |  | B. | 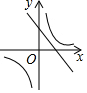 | C. |  | D. |  |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $-\frac{\sqrt{2}}{2}$ | C. | $-\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com