
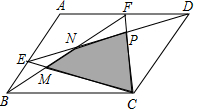
 如圖所示,在平行四邊形ABCD中,E、F分別為AB和AD上的兩個動點.
如圖所示,在平行四邊形ABCD中,E、F分別為AB和AD上的兩個動點.分析 (1)根據平行四邊形的性質,相似三角形的性質以及等底等高的三角形面積相等,進行判斷即可得出面積相等的三角形;
(2)先設△FPN的面積為a,△EMN的面積為b,△BCM的面積為c,△CDP的面積為d,陰影部分面積為s,根據△ADE的面積+△BCE的面積=△CDE的面積,△ABF的面積+△CDF的面積=△BCF的面積,列出等式40+a+16+20+c=b+s+d,40+b+20+16+d=a+s+c,即可求得s的值;
(3)根據DF為AF的$\frac{1}{2}$,且PC是PF的5倍,得出DF:AF=1:2,并設CP=5k,FP=k,則CF=6k,再根據平行線分線段成比例定理,列出比例式,求得PE:PD=PG:PC=(12k+k):5k=13:5,即可得出PE與PD的比值.
解答 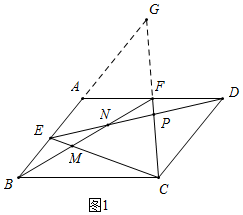 解:(1)如圖1,當點E、F分別為AB,AD的中點時,
解:(1)如圖1,當點E、F分別為AB,AD的中點時,
△ABF的面積=△CDF的面積=△ADE的面積=△BCE的面積=平行四邊形ABCD面積的$\frac{1}{4}$,
△BCF的面積=△CDE的面積=平行四邊形ABCD面積的$\frac{1}{2}$,
如圖所示,延長BA,CF交于點G,
當點E、F分別為AB,AD的中點時,△AFG≌△DFC,故CF=GF,
由CD∥GE可得,△GEP∽△CDP,故CP:GP=2:3,
∴CP:PF=4:1,
同理可得CM:ME=4:1,
∴△CPD的面積=△CDF面積的$\frac{4}{5}$=△BCE面積的$\frac{4}{5}$=△BCM的面積,
∴△FPD的面積=△CDF面積的$\frac{1}{5}$=△BCE面積的$\frac{1}{5}$=△BEM的面積,
又∵△ABF的面積=△ADE的面積,
∴△BEN的面積=△DFN的面積,
∴△MEN的面積=△PFN的面積;
(2)如圖2,設△FPN的面積為a,△EMN的面積為b,△BCM的面積為c,△CDP的面積為d,陰影部分面積為s,則由(1)可得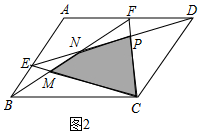
△ADE的面積+△BCE的面積=△CDE的面積,
△ABF的面積+△CDF的面積=△BCF的面積,
即40+a+16+20+c=b+s+d,①
40+b+20+16+d=a+s+c,②
由①+②,可得76=2s,
∴s=38,
即陰影部分面積為38;
(3)如圖1,延長BA,CF交于點G,
∵DF為AF的$\frac{1}{2}$,且PC是PF的5倍,
∴DF:AF=1:2,
設CP=5k,FP=k,則CF=6k,
∵CD∥AG,
∴CF:GF=DF:AF,
即6k:GF=1:2,
∴GF=12k,
∵CD∥EG,
∴PE:PD=PG:PC=(12k+k):5k=13:5,
∴PE與PD的比值為$\frac{13}{5}$.
點評 本題屬于三角形綜合題,主要考查了平行四邊形的性質,相似三角形的判定與性質,三角形的面積計算以及平行線分線段成比例定理的綜合應用,解決問題的關鍵是掌握平行四邊形是中心對稱圖形,并運用相似三角形的對應邊成比例得出線段的比值.


科目:初中數學 來源: 題型:解答題
 如圖,已知正方形ABCD,點E在CB的延長線上,聯結AE、DE,DE與邊AB交于點F,FG∥BE且與AE交于點G.
如圖,已知正方形ABCD,點E在CB的延長線上,聯結AE、DE,DE與邊AB交于點F,FG∥BE且與AE交于點G.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
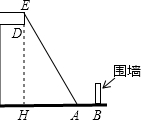 小明的爸爸用10m長的梯子一頭支在地面的A處,一頭正巧擱在屋檐頂部的E處,屋檐板ED為0.9m,A到圍墻底部B的距離為1m,E點的高度EH=8m,小明建議爸爸:“太危險,梯子滑下去就會出事”,爸爸回答:“沒事,梯子左右不滑,上下滑有圍墻擋著呢”,你認為小明爸爸說得對嗎?請你闡述判斷的根據.
小明的爸爸用10m長的梯子一頭支在地面的A處,一頭正巧擱在屋檐頂部的E處,屋檐板ED為0.9m,A到圍墻底部B的距離為1m,E點的高度EH=8m,小明建議爸爸:“太危險,梯子滑下去就會出事”,爸爸回答:“沒事,梯子左右不滑,上下滑有圍墻擋著呢”,你認為小明爸爸說得對嗎?請你闡述判斷的根據.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,某水庫大壩的橫斷面是梯形ABCD,壩頂寬CD=3m,坡角A為30°,壩高DE=8m,壩底寬AB為(27+8$\sqrt{3}$)m,試求迎水坡BC的長和迎水坡BC的坡度.
如圖,某水庫大壩的橫斷面是梯形ABCD,壩頂寬CD=3m,坡角A為30°,壩高DE=8m,壩底寬AB為(27+8$\sqrt{3}$)m,試求迎水坡BC的長和迎水坡BC的坡度.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
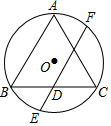 如圖,等邊△ABC內接于⊙O,點D是BC的中點,過點D作AB的平行線交⊙O于點E,F,則$\frac{EF}{BC}$的值是( )
如圖,等邊△ABC內接于⊙O,點D是BC的中點,過點D作AB的平行線交⊙O于點E,F,則$\frac{EF}{BC}$的值是( )| A. | 2 | B. | 1.5 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com