
| x/萬元 | 30 | 80 | 120 |
| y/萬元 | 44 | n | 26 |
分析 (1)設y與x之間的函數關系式為y=kx+b,運用待定系數法就可以求出y與x之間的函數關系式;
(2)設原計劃要m天完成,則增加2km后用了(m+15)天,根據每天修建的工作量不變建立方程求出其解,就可以求出計劃的時間,然后代入(1)的解析式就可以求出結論.
解答 解:(1)設y與x之間的函數關系式為y=kx+b(k≠0),由題意,得$\left\{\begin{array}{l}{44=30k+b}\\{26=120k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-5}\\{b=50}\end{array}\right.$,
∴y與x之間的函數關系式為:y=-$\frac{1}{5}$x+50(30≤x≤120);
(2)設原計劃要m天完成,則增加2km后用了(m+15)天,由題意,得$\frac{6}{m}$=$\frac{6+2}{m+15}$,
解得:m=45,
經檢驗m=45是原方程的根.
∴原計劃每天的修建費為:-$\frac{1}{5}$×45+50=41(萬元).
點評 本題考查了運用待定系數法求函數的解析式的運用,列分式方程解實際問題的運用,設間接未知數在解答應用題的運用,解答時建立分式方程求出計劃修建的時間是關鍵.


科目:初中數學 來源: 題型:選擇題
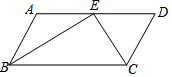 如圖,平行四邊形ABCD中,∠ABC和∠BCD的平分線交于AD邊上一點E,且BE=5,CE=4,則AB的長是( )
如圖,平行四邊形ABCD中,∠ABC和∠BCD的平分線交于AD邊上一點E,且BE=5,CE=4,則AB的長是( )| A. | $\frac{{\sqrt{41}}}{2}$ | B. | 5 | C. | $\sqrt{29}$ | D. | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3(x+1)2=2(x-1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | x2+2x=x2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
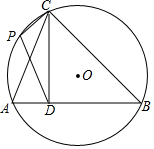 △ABC內接于圓O,CD⊥AB于D,CD=DB=3,AD=1,點P為$\widehat{AC}$上一點,求$\frac{\sqrt{10}}{2}$DP+CP的最小值.
△ABC內接于圓O,CD⊥AB于D,CD=DB=3,AD=1,點P為$\widehat{AC}$上一點,求$\frac{\sqrt{10}}{2}$DP+CP的最小值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
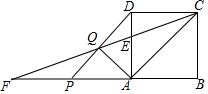 如圖,在正方形ABCD中,AB=3,點E在AD邊上,且DE=$\frac{1}{3}$AD,連結CE并延長交BA的延長線于點F,P是線段AF上一點(點P與點A、F不重合),連結PD,交CF于點Q,設AP=x,CQ=y.
如圖,在正方形ABCD中,AB=3,點E在AD邊上,且DE=$\frac{1}{3}$AD,連結CE并延長交BA的延長線于點F,P是線段AF上一點(點P與點A、F不重合),連結PD,交CF于點Q,設AP=x,CQ=y.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com