Question

1．（1）如圖①，O是等邊△ABC內一點，OA=6，OB=8，OC=10，將線段BO繞點B逆時針旋轉60°得到線段BO'，連結線段OO'，AO'，試判斷△AOO'的形狀．
（2）點D是以AB為斜邊的等腰直角三角形ABC內一點，且BD=1，CD=2，AD=3．
（Ⅰ）求∠BDC的度數；
（Ⅱ）求△ABC的面積．

Answer 1

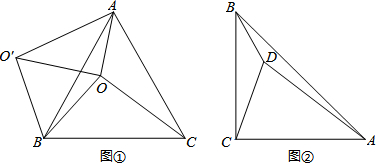
分析 （1）利用旋轉的性質得BO=BO′，∠OBO′=60°，則△OBO′為等邊三角形，所以OO′=OB=8，則可判斷△ABC為等邊三角形，所以∠ABC=60°，BA=BC，接著利用旋轉的定義可把△BOC繞點B逆時針旋轉60°得到△BO′A，于是得到AO′=CO=10，然后根據勾股定理的逆定理可判斷△AOO'為直角三角形，∠AOO′=90°；
（2）（Ⅰ）將△CBD繞點B順時針旋轉90°得到△CAD′，如圖②，根據旋轉的性質得∠DCD′=90°，∠CD′A=∠CDB，CD′=CD=2，AD′=BD=1，則可判斷△CDD′為等腰直角三角形，所以∠CD′D=45°，DD′=$\sqrt{2}$CD=2$\sqrt{2}$，然后根據勾股定理的逆定理可判斷△ADD'為直角三角形，∠AD′D=90°；則∠AD′C=135°，所以∠BDC=135°；
（Ⅱ）利用△CDD′為等腰直角三角形得到∠CDD′=45°，再判斷點B、D、D′共線得到△BD′A為直角三角形，然后利用△ABC的面積=S_△CDD′+S_△BD′A進行計算．

解答 解：（1）∵線段BO繞點B逆時針旋轉60°得到線段BO'，
∴BO=BO′，∠OBO′=60°，
∴△OBO′為等邊三角形，
∴OO′=OB=8，
∵△ABC為等邊三角形，
∴∠ABC=60°，BA=BC，
∴△BOC繞點B逆時針旋轉60°得到△BO′A，
∴AO′=CO=10，
在△AOO′中，∵AO′=10，AO=6，OO′=8，
而6²+8²=10²，
∴OA²+OO′²=AO′²，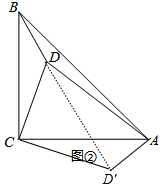
∴△AOO'為直角三角形，∠AOO′=90°；
（2）（Ⅰ）將△CBD繞點B順時針旋轉90°得到△CAD′，如圖②，
∴∠DCD′=90°，∠CD′A=∠CDB，CD′=CD=2，AD′=BD=1，
∴△CDD′為等腰直角三角形，
∴∠CD′D=45°，DD′=$\sqrt{2}$CD=2$\sqrt{2}$，
在△ADD′中，AD=3，AD′=1，DD′=2$\sqrt{2}$，
而1²+（2$\sqrt{2}$）²=3²，
∴D′A²+AD²=DD′²，
∴△ADD'為直角三角形，∠AD′D=90°；
∴∠AD′C=135°，
∴∠BDC=135°；
（Ⅱ）∵△CDD′為等腰直角三角形，
∴∠CDD′=45°，
而∠BDC=135°；
∴∠CDD′+∠BDC=180°，
∴點B、D、D′共線，
∴△BD′A為直角三角形，
∴△ABC的面積=S_△CDD′+S_△BD′A
=$\frac{1}{2}$×2×2+$\frac{1}{2}$×1×（1+2$\sqrt{2}$）
=$\frac{5}{2}$+$\sqrt{2}$．

點評 本題考查了旋轉的性質：對應點到旋轉中心的距離相等；對應點與旋轉中心所連線段的夾角等于旋轉角；旋轉前、后的圖形全等．也考查了等邊三角形的判定與性質和等腰直角直角三角形的判定與性質．