

分析 (1)根據直線MN與直線PQ垂直相交于O可知∠AOB=90°,再由AE、BE分別是∠BAO和∠ABO角的平分線得出∠BAE=$\frac{1}{2}$∠OAB,∠ABE=$\frac{1}{2}$∠ABO,由三角形內角和定理即可得出結論;
(2)由∠BAO與∠BOQ的角平分線相交于E可知∠EAO=$\frac{1}{2}$∠BAO,∠EOQ=$\frac{1}{2}$∠BOQ,進而得出∠E的度數,由AE、AF分別是∠BAO和∠OAG的角平分線可知∠EAF=90°,在△AEF中,由一個角是另一個角的3倍分四種情況進行分類討論.
解答  解:(1)∠AEB的大小不變,
解:(1)∠AEB的大小不變,
∵直線MN與直線PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分別是∠BAO和∠ABO角的平分線,
∴∠BAE=$\frac{1}{2}$∠OAB,∠ABE=$\frac{1}{2}$∠ABO,
∴∠BAE+∠ABE=$\frac{1}{2}$(∠OAB+∠ABO)=$\frac{1}{2}$×90°=45°,
∴∠AEB=135°;
(2)∵AE、AF分別是∠BAO和∠OAG的角平分線,
∴∠EAO=$\frac{1}{2}$∠BAO,∠FAO=$\frac{1}{2}$∠GAO,
∴∠EAF=$\frac{1}{2}$(∠BAO+∠GAO)=$\frac{1}{2}$×180°=90°.
故答案為:90;
∵∠BAO與∠BOQ的角平分線相交于E,
∴∠EAO=$\frac{1}{2}$∠BAO,∠EOQ=$\frac{1}{2}$∠BOQ,
∴∠E=∠EOQ-∠EAO=$\frac{1}{2}$(∠BOQ-∠BAO)=$\frac{1}{2}$∠ABO,
即∠ABO=2∠E,
在△AEF中,∵有一個角是另一個角的3倍,故分四種情況討論:
①∠EAF=3∠E,∠E=30°,則∠ABO=60°;
②∠EAF=3∠F,∠E=60°,∠ABO=120°(舍去);
③∠F=3∠E,∠E=22.5°,∠ABO=45°;
④∠E=3∠F,∠E=67.5°,∠ABO=135°(舍去).
∴∠ABO為60°或45°.
點評 本題考查的是三角形內角和定理、三角形外角性質以及角平分線的定義的運用,熟知三角形內角和是180°是解答此題的關鍵.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | 3cm,5cm,8cm | B. | 8cm,7cm,13cm | C. | 13cm,12cm,31cm | D. | 7cm,7cm,15cm |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
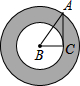 如圖,在Rt△ABC中,∠C=90°,將其繞B點順時針旋轉一周,則分別以BA,BC為半徑的圓形形成一圓環(huán)(陰影部分),為求該圓環(huán)的面積,只需測量一條線段的長度,這條線段就是( )
如圖,在Rt△ABC中,∠C=90°,將其繞B點順時針旋轉一周,則分別以BA,BC為半徑的圓形形成一圓環(huán)(陰影部分),為求該圓環(huán)的面積,只需測量一條線段的長度,這條線段就是( )| A. | AD | B. | AB | C. | BD | D. | AC |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 運算程序 | 例如 | 按左側的形式完成你的舉例 |
| ①給出任意一個三位數 | 325 | 123 |
| ②重復①中的數,得到一個新的數字 | 325325 | 123123 |
| ③將②的結果除以7 | 325325÷7=a46475 | 123123÷7=17589 |
| ④將③的結果除以11 | a÷11=b4225 | 17589÷11=1599 |
| ⑤將④的結果除以13 | b÷13=325 | 1599÷13=123 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 單項式$\frac{1}{2}$xy的系數是$\frac{1}{2}$,次數是1 | |
| B. | 單項式-$\frac{1}{3}$πa2b3的系數是-$\frac{1}{3}$,次數是6 | |
| C. | 單項式x2的系數是1,次數是2 | |
| D. | 多項式2x3-3x2y2+x-1叫三次四項式 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com