
 已知:如圖,在△ABC中,點D,E分別在邊AB,BC上,BA•BD=BC•BE
已知:如圖,在△ABC中,點D,E分別在邊AB,BC上,BA•BD=BC•BE分析 (1)由BA•BD=BC•BE得$\frac{AB}{BC}=\frac{BE}{BD}$,結合∠B=∠B,證△ABC∽△EBD得$\frac{AB}{BE}=\frac{AC}{ED}$,即可得證;
(2)先根據AC2=AD•AB證△ADC∽△ACB得∠ACD=∠B,再由$\frac{AB}{BC}=\frac{BE}{BD}$證△BAE∽△BCD得∠BAE=∠BCD,根據∠AEC=∠B+∠BAE,∠ACE=∠ACD+∠BCD可得∠AEC=∠ACE,即可得證.
解答 證明:(1)∵BA•BD=BC•BE,
∴$\frac{AB}{BC}=\frac{BE}{BD}$,
又∵∠B=∠B,
∴△ABC∽△EBD,
∴$\frac{AB}{BE}=\frac{AC}{ED}$,
∴DE•AB=AC•BE;
(2)∵AC2=AD•AB,
∴$\frac{AC}{AD}=\frac{AB}{AC}$,
∵∠DAC=∠CAB,
∴△ADC∽△ACB,
∴∠ACD=∠B,
∵$\frac{AB}{BC}=\frac{BE}{BD}$,∠B=∠B,
∴△BAE∽△BCD,
∴∠BAE=∠BCD,
∵∠AEC=∠B+∠BAE,∠ACE=∠ACD+∠BCD,
∴∠AEC=∠ACE,
∴AE=AC.
點評 本題主要考查相似三角形的判定與性質,熟練掌握兩邊對應成比例且夾角相等的兩三角形相似是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{2}{sinα}$ | B. | 2sinα | C. | $\frac{2}{cosα}$ | D. | 2cosα |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (3,4) | B. | (1,2) | C. | (3,2) | D. | (1,4) |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
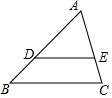 如圖,點D、E位于△ABC的兩邊上,下列條件能判定DE∥BC的是( )
如圖,點D、E位于△ABC的兩邊上,下列條件能判定DE∥BC的是( )| A. | AD•DB=AE•EC | B. | AD•AE=BD•EC | C. | AD•CE=AE•BD | D. | AD•BC=AB•DE |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,小明家所在小區的前后兩棟樓AB、CD,小明在自己所住樓AB的底部A處,利用對面樓CD墻上玻璃(與地面垂直)的反光,測得樓AB頂部B處的仰角是α,若tanα=0.45,兩樓的間距為30米,則小明家所住樓AB的高度是27米.
如圖,小明家所在小區的前后兩棟樓AB、CD,小明在自己所住樓AB的底部A處,利用對面樓CD墻上玻璃(與地面垂直)的反光,測得樓AB頂部B處的仰角是α,若tanα=0.45,兩樓的間距為30米,則小明家所住樓AB的高度是27米.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com