
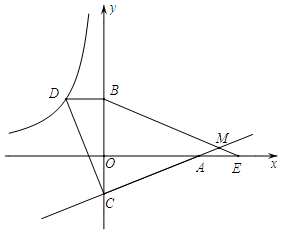
 如圖,已知點(diǎn)D在反比例函數(shù)y=$\frac{m}{x}$的圖象上,過點(diǎn)D作x軸的平行線交y軸于點(diǎn)B(0,3).過點(diǎn)A(5,0)的直線y=kx+b與y軸于點(diǎn)C,且BD=OC,tan∠OAC=$\frac{2}{5}$.
如圖,已知點(diǎn)D在反比例函數(shù)y=$\frac{m}{x}$的圖象上,過點(diǎn)D作x軸的平行線交y軸于點(diǎn)B(0,3).過點(diǎn)A(5,0)的直線y=kx+b與y軸于點(diǎn)C,且BD=OC,tan∠OAC=$\frac{2}{5}$.分析 (1)由A點(diǎn)坐標(biāo)可求得OA的長,再利用三角函數(shù)的定義可求得OC的長,可求得C、D點(diǎn)坐標(biāo),再利用待定系數(shù)法可求得直線AC的解析式;
(2)由條件可證明△OAC≌△BCD,再由角的和差可求得∠OAC+∠BCA=90°,可證得AC⊥CD;
(3)連接AD,可證得四邊形AEBD為平行四邊形,可得出△ACD為等腰直角三角形,則可求得答案.
解答 解:
(1)∵A(5,0),
∴OA=5.
∵$tan∠OAC=\frac{2}{5}$,
∴$\frac{OC}{OA}=\frac{2}{5}$,解得OC=2,
∴C(0,-2),
∴BD=OC=2,
∵B(0,3),BD∥x軸,
∴D(-2,3),
∴m=-2×3=-6,
∴$y=\frac{-6}{x}$,
設(shè)直線AC關(guān)系式為y=kx+b,
∵過A(5,0),C(0,-2),
∴$\left\{\begin{array}{l}0=5k+b\\-2=b\end{array}\right.$,解得$\left\{\begin{array}{l}k=\frac{2}{5}\\ b=-2\end{array}\right.$,
∴$y=\frac{2}{5}x-2$;
(2)∵B(0,3),C(0,-2),
∴BC=5=OA,
在△OAC和△BCD中
$\left\{\begin{array}{l}{OA=BC}\\{∠AOC=∠DBC}\\{OC=BD}\end{array}\right.$
∴△OAC≌△BCD(SAS),
∴AC=CD,
∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD;
(3)∠BMC=45°.
如圖,連接AD,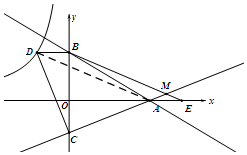
∵AE=OC,BD=OC,AE=BD,
∴BD∥x軸,
∴四邊形AEBD為平行四邊形,
∴AD∥BM,
∴∠BMC=∠DAC,
∵△OAC≌△BCD,
∴AC=CD,
∵AC⊥CD,
∴△ACD為等腰直角三角形,
∴∠BMC=∠DAC=45°.
點(diǎn)評(píng) 本題為反比例函數(shù)的綜合應(yīng)用,涉及待定系數(shù)法、全等三角形的判定和性質(zhì)、平行四邊形的判定和性質(zhì)、等腰直角三角形的判定和性質(zhì)等知識(shí).在(1)中求得C、D的坐標(biāo)是解題的關(guān)鍵,在(2)中證得△OAC≌△BCD是解題的關(guān)鍵,在(3)中證明四邊形AEBD為平行四邊形是解題的關(guān)鍵.本題考查知識(shí)點(diǎn)較多,綜合性較強(qiáng),難度適中.


 期末好成績系列答案
期末好成績系列答案 99加1領(lǐng)先期末特訓(xùn)卷系列答案
99加1領(lǐng)先期末特訓(xùn)卷系列答案 百強(qiáng)名校期末沖刺100分系列答案
百強(qiáng)名校期末沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
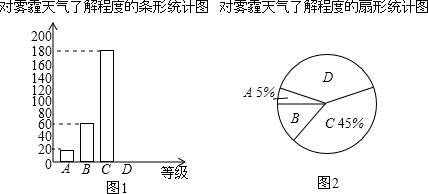
| 對(duì)霧霾的了解程度 | 百分比 |
| A.非常了解 | 5% |
| A.比較了解 | 15% |
| C.基本了解 | 45% |
| D.不了解 | n |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
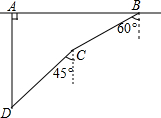 如圖,一次軍事演習(xí)中,藍(lán)方在-條東西走向的公路上的A處朝正南方向撤退,紅方在公路上的B處沿南偏西60°方向前進(jìn)實(shí)施攔截.紅方行駛2000米到達(dá)C后,因前方無法通行,紅方?jīng)Q定調(diào)整方向,再朝南偏西45°方向前進(jìn)了相同距離,剛好在D處成功攔截藍(lán)方.
如圖,一次軍事演習(xí)中,藍(lán)方在-條東西走向的公路上的A處朝正南方向撤退,紅方在公路上的B處沿南偏西60°方向前進(jìn)實(shí)施攔截.紅方行駛2000米到達(dá)C后,因前方無法通行,紅方?jīng)Q定調(diào)整方向,再朝南偏西45°方向前進(jìn)了相同距離,剛好在D處成功攔截藍(lán)方.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
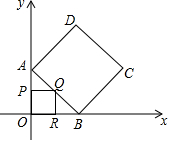 如圖,在直角坐標(biāo)系中,已知A(0,4)、B(4,0),以AB為邊在第一象限內(nèi)作正方形ABCD,在三角形AOB內(nèi)部做正方形OPQR,使P、R、Q三點(diǎn)分別在線段OA、OB、AB上,將正方形OPQR繞點(diǎn)O順時(shí)針旋轉(zhuǎn)時(shí),求點(diǎn)C到點(diǎn)Q距離的最大值與最小值.
如圖,在直角坐標(biāo)系中,已知A(0,4)、B(4,0),以AB為邊在第一象限內(nèi)作正方形ABCD,在三角形AOB內(nèi)部做正方形OPQR,使P、R、Q三點(diǎn)分別在線段OA、OB、AB上,將正方形OPQR繞點(diǎn)O順時(shí)針旋轉(zhuǎn)時(shí),求點(diǎn)C到點(diǎn)Q距離的最大值與最小值.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
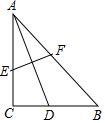 如圖,在Rt△ABC中,∠C=90°,AC=BC,AD是BC邊上的中線,將A點(diǎn)翻折與點(diǎn)D重合,得到折痕EF,則$\frac{CE}{AE}$=$\frac{3}{5}$.
如圖,在Rt△ABC中,∠C=90°,AC=BC,AD是BC邊上的中線,將A點(diǎn)翻折與點(diǎn)D重合,得到折痕EF,則$\frac{CE}{AE}$=$\frac{3}{5}$.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com