
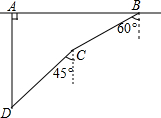
 如圖,一次軍事演習中,藍方在-條東西走向的公路上的A處朝正南方向撤退,紅方在公路上的B處沿南偏西60°方向前進實施攔截.紅方行駛2000米到達C后,因前方無法通行,紅方決定調整方向,再朝南偏西45°方向前進了相同距離,剛好在D處成功攔截藍方.
如圖,一次軍事演習中,藍方在-條東西走向的公路上的A處朝正南方向撤退,紅方在公路上的B處沿南偏西60°方向前進實施攔截.紅方行駛2000米到達C后,因前方無法通行,紅方決定調整方向,再朝南偏西45°方向前進了相同距離,剛好在D處成功攔截藍方.分析 過B作AB的垂線,過C作AB的平行線,兩線交于點E;過C作AB的垂線,過D作AB的平行線,兩線交于點F,則∠E=∠F=90°;
(1)點C到公路的距離就是BE的長,在Rt△BCE中,根據三角函數可求BE的長.
(2)紅藍雙方相距AB=DF+CE.在Rt△BCE中,根據銳角三角函數的定義求出CE的長,同理,求出DF的長,進而可得出結論.
解答 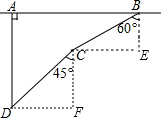 解:過B作AB的垂線,過C作AB的平行線,兩線交于點E;過C作AB的垂線,過D作AB的平行線,兩線交于點F,則∠E=∠F=90°,
解:過B作AB的垂線,過C作AB的平行線,兩線交于點E;過C作AB的垂線,過D作AB的平行線,兩線交于點F,則∠E=∠F=90°,
(1)點C到公路的距離就是BE的長,
在Rt△BCE中,∵BC=2000米,∠EBC=60°,
∴BE=BC•cos60°=2000×$\frac{1}{2}$=1000米.
答:點C到公路的距離就是BE的長是1000米.
(2)紅藍雙方相距AB=DF+CE.
在Rt△BCE中,
∵BC=2000米,∠EBC=60°,
∴CE=BC•sin60°=2000×$\frac{\sqrt{3}}{2}$=1000$\sqrt{3}$米.
在Rt△CDF中,
∵∠F=90°,CD=2000米,∠DCF=45°,
∴DF=CD•sin45°=2000×$\frac{\sqrt{2}}{2}$=1000$\sqrt{2}$米,
∴AB=DF+CE=(1000$\sqrt{2}$+500$\sqrt{3}$)米.
答:紅藍雙方最初相距(1000$\sqrt{2}$+1000$\sqrt{3}$)米.
點評 本題考查了解直角三角形的應用-方向角問題,銳角三角函數的定義,正確理解方向角的定義,進而作出輔助線構造直角三角形是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 組號 | 分組 | 頻數 |
| 一 | 9.6≤x<9.7 | 1 |
| 二 | 9.7≤x<9.8 | 2 |
| 三 | 9.8≤x<9.9 | a |
| 四 | 9.9≤x<10 | 8 |
| 五 | x=10 | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,一次函數與反比例函數y=$\frac{m}{x}$的圖象交于A(1,4),B(4,n)兩點.
如圖,一次函數與反比例函數y=$\frac{m}{x}$的圖象交于A(1,4),B(4,n)兩點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
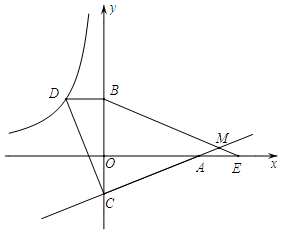 如圖,已知點D在反比例函數y=$\frac{m}{x}$的圖象上,過點D作x軸的平行線交y軸于點B(0,3).過點A(5,0)的直線y=kx+b與y軸于點C,且BD=OC,tan∠OAC=$\frac{2}{5}$.
如圖,已知點D在反比例函數y=$\frac{m}{x}$的圖象上,過點D作x軸的平行線交y軸于點B(0,3).過點A(5,0)的直線y=kx+b與y軸于點C,且BD=OC,tan∠OAC=$\frac{2}{5}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com