
| x | 3 | 5 |
| y | 18 | 14 |
分析 (1)根據題意設出銷售量y件與日銷售單價x元之間的函數表達式,然后根據題目中的數據即可求得函數解析式;
(2)根據題意和(1)中的函數解析式即可用含x的代數式表示出P,然后將P的關系式化為頂點式即可解答本題.
解答 解:(1)設銷售量y件與日銷售單價x元之間的函數表達式是y=kx+b,
$\left\{\begin{array}{l}{3k+b=18}\\{5k+b=14}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-2}\\{b=24}\end{array}\right.$,
∴銷售量y件與日銷售單價x元之間的函數表達式是y=-2x+24;
(2)由題意可得,
P=x(-2x+24)=-2x2+24x=-2(x-6)2+72,
∴日銷售利潤P元與日銷售單價x元之間的函數表達式是P=-2x2+24x,當日銷售單價x為6元時,才能獲得最大日銷售利潤.
點評 本題考查二次函數的應用,解答此類問題的關鍵是明確題意,求出相應的函數解析式,利用二次函數的頂點式求函數的最值.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
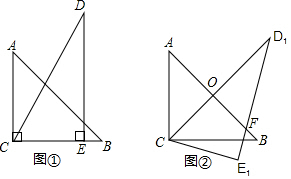
| A. | 10° | B. | 15° | C. | 7.5° | D. | 20° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2cm,3cm,5cm | B. | 5cm,6cm,10cm | C. | 1cm,1cm,3cm | D. | 2cm,4cm,8cm |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com